| ��P |
�퍐��P�}�Ȃ�����S�}�ɂ��� |
| �@�P |
�������z�}�Ɋւ���퍐�̊�{�I�ȊԈႢ |
|
(1) |
�퍐�̓R�A�̌`��Ǝ������z�T�O�̐����̂��߂̎����}�Ƃ��Ĕ퍐�������ʁi�R�j�Q�O�ňȍ~�ɑ�P�}�Ȃ�����S�}�������B |
|
|
�������A�����̐}�͊����ɗ����d����S���z�����Ă��Ȃ��Ƃ����A����߂Ċ�{�I�ȃ~�X��Ƃ��Ă���B
�����炭�퍐�͎��C�V�~�����[�V�����Ƃ����t�F���C�g�R�A�W�̉�̓\�t�g��p���Ă��̃V�~�����[�V�������ʂ����̂ł���Ǝv����B
�������A�����̃\�t�g�͌������m�F�����Ƃ���A�����݂̂̂�P�ƂŃV�~�����[�V�������Ă�����̂������A���݂̂Ƃ��늪���ɗ����d�����ɍl�����鎥�C�V�~�����[�V�����\�t�g�͎s�̂���Ă��Ȃ������肪���ɍ���ȏɂ���͂��ł���B |
|
(2) |
�퍐�͔퍐�̎������C�V�~�����[�V�������������Ǝ咣����̂ł���A�����Ɠ����悤�ɔ��ɊȒP�Ȏ��؎������s���āA�퍐�̎��C�V�~�����[�V�����������ƓK������̂������Ȃ���ΈӖ����Ȃ��B |
|
|
�Ȃ��A�b��P�U���ؐ}�Q�́i�Q�j�����̑[�u�}�A���邢�͍b�P�V���ؐ}�V�A����ɁA�u���̎����̈Ӗ��v�Ƃ��āA�������s�������؎����́A�t�@���f�[�E�m�C�}���̖@���Ɋ�Â�����߂Ċ�{�I�Ȏ������@�ł��邱�Ƃ�������������Ă���B
�퍐�́A���̎������@�Ɋւ��Ĕ۔F���邱�Ƃ̓t�@���f�[�E�m�C�}���̖@���ɂ��Ĕ۔F���邱�Ƃɓ��������ߔ۔F�ł����A����ɘk���N���b�v��p�������Ƃɑ��Ĕᔻ���Ă��邪�A����Ȃ�Δ퍐���g���K���Ƃ���悤�ɒ[�q���͂t������Ȃ肵�Ĕ퍐�������ʁi�R�j�Q�O�ňȍ~�̐}�P�Ȃ����}�S�Ɏ������C����̎��؎������s�Ȃ��悢�B |
| �@�Q |
���C�V�~�����[�V�����\�t�g�̖��_ |
|
���ɁA�����ɗ����d�����l���ł��Ȃ����C�V�~�����[�V�����\�t�g��p�����ꍇ�Ɋׂ�₷�����_�ɂ��ďq�ׂ�B |
|
(1) |
�܂��A�퍐�������ʁi�R�j��Q�}�ɂ��Ă̐����Ɂu�ꎟ�����͊J�����v�i�����{�������ʐ}�P�|�P�������j�Ƃ��邪�A�����������A�C���o�[�^��H���V�~�����[�V��������Ȃ�Έꎟ�����͒Z���łȂ���Ȃ�Ȃ��B |
|
|
�}1-1 |
�唼�̎����ސ�p�̎��C�V�~�����[�V�����\�t�g�ł͂��������������Z�����̃V�~�����[�V�����@�\�͗L���Ă��Ȃ��B
�ꎟ�������Z����Ԃł���ƁA�����͈ꎟ�����𗬂��d���ɂ���Ĉꎟ�����Ɋѓ��ł��Ȃ����A���邢�͊ѓ����������͈ꎟ�������т��Ȃ���Ȃ�Ȃ��B
���̎��C�V�~�����[�V�����i�Ԑ��Ŏ��������́j�̊ԈႢ�ɂ���Ă��̌�̑�R�}���A��S�}���Ȃǂ��̌�̑S�Ă̌��ɂȂ����Ă���B
���Ȃ݂ɂȂ��ꎟ�����͒Z���łȂ���Ȃ�Ȃ��̂��Ƃ����ƁA�T�����q�ׂ����́u�𗬓I�ɒZ���v����Ă��邱�Ƃł���B
�}�P�|�Q�͉���V����figure20������p���Ă���MP-1010��IC�̏o�͕��̃g�����W�X�^�Ƃ���ɐڑ������g�����X�A��A�Ɋǂ̉�H�}�ł���B |
|
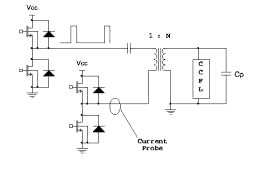 |
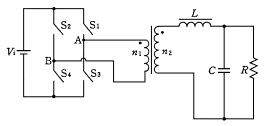 |
�}1-2
����V����figre20��� |
�}1-3
�𗬓I������H |
|
|
|
�����Ɏ������g�����W�X�^�̓X�C�b�`���O�����������̂ł���i�}�P�|�R�j�A��ɓd��������GND�ɐڑ�����Ă��邩�A�ǂ���ɂ��ڑ�����Ă��Ȃ��ꍇ��GND���̃g�����W�X�^���m�����ʂ��ĒZ����ԂɂȂ�B
�d�������GND�ɐڑ�����Ă���ꍇ�̃C���s�[�_���X�͂����܂ł��Ȃ�0���ł��邩��A���ǃX�C�b�`���O����ɂ�����ꎟ�����͌𗬓I�ɂ͏�ɒZ����Ԃɂ���킯�ł���B
�����̂��Ƃ́A�X�C�b�`���O���������d����H�ł͏펯�I�Ȃ��Ƃł���̂ł���ȏ�̐����͗v���Ȃ��ł��낤�B�퍐�͂��̂悤�Ȃ���߂Ċ�{�I�Ȏ����Ɋւ��Ă����P�����Ɏ咣���q�ׂĂ���̂ł���B |
|
(2) |
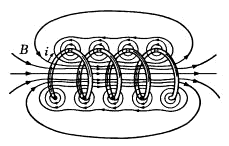
�}1-4
�\���m�C�h��ʂ蔲���鎥�� |
�����͔퍐�����̂悤�Ȋ�{�I�Ȍ���Ƃ��Ȃ��悤�ɁA���炩���ߊ����𗬂��d���ɂ���Đ����鎥�E�͈�l�ŕ��s���E�ł���Ɛ������Ă��镶�����������i�b��W���P�R�R�Ő}6.5�j�B�\���m�C�h��������������͂��낢��Ƃ��邪�A����d�C���C�w�i���C�X���o�ŎЁj�Ɏ��������̂��ł������I�ŏڍׂł��낤�Ǝv����̂Ő}�P�|�S�Ɏ����B |
|
|
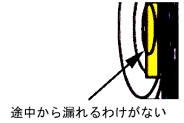
�}1-5 |
���z�萔���������ł���ꍇ�A�����̂������[�������Ď��E�͊������т����̂ł���A��{�I�Ɋ����̓r������R��o�����̂ł͂Ȃ��B�}�P�|�T�Ɏ����悤�ɔ퍐���퍐�������ʁi�R�j�Q�O�ňȍ~�̐}�P�Ȃ����}�S�Ɏ����悤�Ȋ����r������̎����R��́A�������W���萔��Ƃ������Ȃ��Ȃ��ꎟ������ł͂��蓾�Ȃ��̂ł���B���������āA������邱���̐}�͐������͐}�P�|�U�̂悤�ɏ������߂��Ȃ���Ȃ�Ȃ��B
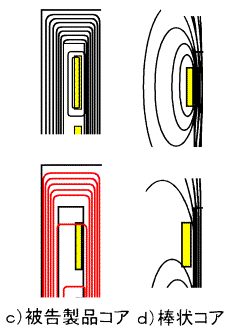
�}1-6 �ꎟ�����ߖT�̎��� |
�܂��A������ɂ����鎥���R�ꂪ�����錻�ۂɂ��Ă͔퍐���q�ׂ�퍐�������ʁi�R�j��Q�}��Ŏ������悤�ȒP���Ȏ��C�R��ł͌����ĂȂ��B
�Ȃ��Ȃ�A���̐}�Ŏ�����鎥���R��͓����ɗ����d���ɂ��e����S���z�����Ă��Ȃ��B�����̕��z�萔���������ł���Ƃ���Ȃ�A�����̐}�ɂ����Ă��A�������������т��悤�Ɏ�����Ă��Ȃ���Ȃ�Ȃ����A�����ɓd�������������Ŏ����R�ꂪ�N����̂ł������͓����̕��z�萔���������ł��Ȃ�����ł���B����́A������̊e���ʂ��Ƃɓ����ɗ����d�����قȂ��Ă���Ƃ������Ƃł���A��{�̓�����ł��̂悤�Ȃ��Ƃ��N����Ƃ���Ί����Ԃɑ��݂���e�ʁi�܂�͕��z�e�ʁj��ʂ��ēd��������Ă��邱�Ƃł���A���Ȃ킿���z�萔��ł��邱�Ƃ��Ӗ�����̂ł���B
�⑫�ł��邪�A�ꎟ�����͊����������Ȃ������ԕ��z�e�ʂ����Ȃ��̂ŃC���o�[�^�̓�����g���i��60��Hz�j�ɂ����ĕ��z�萔���͖����ł���B
����ɔ�ׁA�����͊��������������ԕ��z�e�ʂ������̂ŁA�C���o�[�^�̓�����g���i��60��Hz�j�ɂ����ĕ��z�萔���������ł��Ȃ��̂ł���B |
|
(3) |
�}�P�|�U������Ζ��炩�Ȃ悤�ɁA�O���R�A�����݂���ꍇ�Ƃ����łȂ��ꍇ�Ƃ��ׂĂ��A�O���R�A�͒��S�R�A�̎��H����R��o���������̒ʘH���`�����Ă��邾���ɉ߂��Ȃ��̂ł���A�O���R�A�̂���Ȃ��ɂ�����炸�A���S�R�A�𗬂�鎥���̐���i���Ȃ킿�A�ꎟ�����A�����̂��ꂼ��ɍ������鎥���̐���j�Ɋ�{�I�ȍ��͂Ȃ��B�g�����X�̏�����p�͈ꎟ�����A�����Ƃ���ɍ������鎥���Ƃ̑��ݍ�p���S�Ăł���̂�����A����ȊO�̕����i�O���R�A�j�̎������ǂ����낤�Ɩ{���_�ɂ͑S�R�e���Ȃ��̂ł���B |
| �@�R |
�g�����X�^�]���̎������z�T�O�} |
|
�Ȃ��A�퍐�������ʁi�R�j��R�}�̉��i�ɋL�ڂ��Ă�������͈�ʓI�ȃg�����X�̓d�͕ϊ��ɂ��ċL�ڂ������̂ɉ߂��Ȃ��̂ł��邪�A�����̋Z�p�̐����Ɏ�����_���L�q����Ă���̂ŁA���̓_�ɂ��ĕ⑫����B
����́A�u��ʂɗ㎥�����i�厥���j�ƕ������i���ׂɗ����d���ɂ�����鎥���܂�͘R�ꎥ���ƍl���Ă悢�j�͕��ׂɂ��d�C�I�Ȉʑ����قȂ邪�i�܂�A��R�����ׂɂ�蔭�����镉�����͗㎥��������90�x�x���j�A�ꎟ�����Ɠ������דd���ɂ�鎥���݂͌��ɋt�����ɂȂ��Ă���i���R�k�����ƈꎟ���R�k�����Ƃ݂͌��ɋt�����ɂȂ��Ă���A�܂�ꎟ���R�k�����͎厥������90�x�i��ł���j�B�v�Ƃ������Ƃł���B
�����ŏq�ׂĂ��邱�Ƃ́A�]���̃g�����X�ł͈ꎟ�������ɔ�������㎥�����i�厥���j�ƕ������i�R�k�����j�Ƃ��x�N�g�����������ꍇ�A�ʑ���90�x����Ă���̂ł��邩�獇�v���������̐�Βl�͕K���i�킸���Ɂj������X���ɂ���B
�������A�{�������Z�p�̏ꍇ�A�����������ʂS�̂P�V�łȂ����P�X�łŐ��������Ƃ���A�ꎟ�����ߖT�̎����ʑ��͓����̈ꎟ�������牓�[���̎����ʑ�����90�x�i��ł���̂ł��邩��ꎟ�����ɔ�������R�k�����i�������j�͎厥���Ƃ��傤�Njt�ʑ��ƂȂ�B
���������āA�厥���ƕ������Ƃ̍��������͂킸���Ɍ���X���ɂ���Ƃ����_�ŏ]���̃g�����X�ƈقȂ�̂ł���B |
| �@�S |
�퍐���i���R�k�����^�ł���Ƃ������� |
|
�퍐�͔퍐�������ʁi�R�j��R�}d)�ɂ����āA�u�㎥�����ʂ����������ʂ������Ƃ��́A�����̎�̂͘R�ꎥ���ɂȂ�v�Əq�ׂĂ��邪�A���̋L�q�������āA�퍐�͔퍐���i�Ɏg���Ă���g�����X���R�k�����^�i�]���̘R�k�����^���{�������̘R�k�����^���͕ʂƂ��āj�ł��邱�Ƃ�����F�߂Ă���B�����������H�^�i��R�k�����^�j�g�����X�Ƃ������̂͂��̂悤�ȏ������ł͎g���Ȃ����̂Ȃ̂ł���B���̓_�́A�퍐�������ʁi�R�j�P�U�Łi�S�j�ȍ~�u�O�̈w�E����ƁA�ǎ����^�g�����X�́A��ΓI�ȘR�ꎥ���ʂ̏��Ȃ��g�����X���Ӗ�������̂ł͂Ȃ��v�Ƃ����L�ڂ�������炩�ł���B
������ɂ��Ă��A�퍐���i�̃C���o�[�^�Ɏg���Ă���g�����X���R�k�����^�ł���Ƃ����؋��́A���Y�L�q�ȊO�ɂ��������o���Ă���̂ŘR�k�����^�������łȂ����ɂ��Ă̋c�_�͂��͂⌋�_���o�Ă�����̂Ǝv����B |
| ��Q |
�u��P�@�{�����������̗v�����߂ɂ��āv�ɂ��� |
| �@�P |
�{�����������̗v���`�ɂ��� |
|
(1) |
��L�ɂ��ẮA���Ɍ����������ʂS�A�S�łȂ����U�łɂ����Ĕ��_���Ă���A�퍐�������ʁi�R�j�ɂ�����V���Ȏ咣�ɂ̂ݒlj�����B |
|
(2) |
�퍐�͔퍐�������ʁi�R�j��1�}�ɂ����āA�R�A�̌`�퍐���i�̂n�h�^�R�A�ȊO�̂d�d�^�R�A��d�h�^�R�A�ɂ����Ă������̐����l�ɂȂ�Ƃ������Ƃ��q�ׂĂ��邪�A���������{�����������ɏq�ׂĂ���d�d�^�R�A��d�h�^�R�A�Ƃ͖{�����o�蓖���i�P�X�X�R�N�W���j�ɑ��݂��Ă����i�h�r�W���^������ɋ߂��`��̂d�d�^�R�A��d�h�^�R�A�ł���B |
|
|
�i�h�r�W���^�d�d�R�A��d�h�R�A�̓R�A�f�ʐςɔ�ׂĎ����̒ʂ蓹�i���H�j�̒������Ȃ�ׂ����Ȃ��Ȃ�悤�ɔz������Đv���ꂽ���̂ł���A�d�d�R�A��d�h�R�A�Ƃ����Ύ����R�ꂪ���Ȃ����̂ł���Ƃ����̂������̓��Ǝ҂̒ʔO�ł���B�܂��A���̂��Ƃ͖{�����������̒��ɂ��A�u�y0002�z�܂��A���d�Ǘp�C���o�[�^�[��H�ɗp�����鏸���g�����X�̃R�A�`��́A�����̘R���������L�Q�ƕ߂炦���{�v������H�^�A�܂�A�d�h�^�����͂d�d�^���̗p����邱�Ƃ����������B�v�Əq�ׂĂ���̂ł��邩��A�{�������ɏq�ׂ�d�h�^�y�тd�d�^�R�A�Ƃ͎����R��̏��Ȃ��R�A�\���Ɍ��肳��邱�Ƃ͖����ł���B���Ȃ킿�A�ŋ߂̂悤�Ɏ����R����Ӑ}���ăR�A�f�ʐςɔ�ׂi�h�r�W���^�����ɒ[�Ɏ��H�̒������������̂́A�������݂��Ȃ������̂ł���B�{�����������ɂ�����u�A��������{�̖_��R�A�v�́A���̓_������߂��Ȃ���Ȃ�Ȃ��B
���������āA�{�����������̍\���v����A�퍐���i�̂悤�Ȍ`��̊O��������R�A�́A�P�Ȃ�t�����ɉ߂��Ȃ��B |
| �@�Q |
�{�����������̗v���c�ɂ��� |
|
��L���A�����W���ɂ��ẮA���ɁA�����������ʂS�A�u��T�@�����W���ɂ��āv�i�S�R�ňȍ~�j�Ŕ��_���Ă��邪�A�퍐�������ʁi�R�j�ɔ��_���邽�߁A����ɂ��Ă͌�q����B |
| �@�R |
�{�����������̗v���d�P�ɂ��� |
|
��L�ɂ��Ă��A���ɁA�����������ʂQ�A�V�łȂ����P�O�ŁA�����������ʂS�A�U�łȂ����V�łɂ��Đ����ς݂ł���B
��L�ɂ��Ă̔퍐�̎咣�́A����V���Ȏ咣���܂�ł��Ȃ��B |
| �@�S |
�{�����������̗v���d�Q�ɂ��� |
|
��L�̂����A�e�ʂɂ��ẮA��q����B |
| �@�T |
�{�����������̗v���d�R�ɂ��� |
|
���U��H�ƒ��U���g���ɂ��ẮA��q����B |
| ��R |
�u��R�@�퍐���i�ɂ��āv�ɑ��锽�_ |
| �@�P |
�u�P�@�퍐���i�̉�H����ɂ��āv |
|
(1) |
�퍐�́A�퍐���i�̉�H����ɂ����~�~�������s���A�퍐���i�ɂ����Ă͒��U���g����46kHz���x�ł���A������g������62kHz�`��65kHz�ł��邩��A���U���g�����������ƍ������g���œ��삳���Ă���|�咣����B |
|
|
�X�ɁA�퍐���i�ɂ����ẮA�����g���J�b�g���邽�߂Ƀo���h�p�X�t�B���^�[��H���̗p���Ă���|�咣����B
�܂��A�퍐�́A�퍐���i�͕��d�ǂ��t���p�l��������O�����ɂ��A�e�ʂ���菜���Ă��A�C���o�[�^��H�͐���ɓ��삷�邵�A�e�ʂ����邱�Ƃɂ��]���ȓd�͏�������Ă���|�咣����B |
|
(2) |
�������A�퍐�̏�q����咣�́A���ꂼ��A���ł���B |
|
|
�����̌��ɂ��ẮA���̗��R�ɂ��Ă��ڂ����q�ׂ�K�v������̂ŁA�X�̔F�۔��_�ł͂Ȃ��A��q���錴���̔��_�Ɋ܂߂���̂Ƃ���B |
| �@�Q |
�u�Q�@�{�����������̗v���`�Ƃ̑Δ�v |
|
(1) |
�퍐���咣����R�k�����������W���ŕ\���Ƃ����咣�����ł��邱�Ƃ́A���ɁA�����������ʂS�A�u��T�@�����W���ɂ��āv�i�S�R�ňȍ~�j�Ŕ��_���Ă��邪�A�퍐�������ʁi�R�j�ɔ��_���邽�߁A�{�������ʌ㔼�ɂ����čēx�ڏq����B |
|
|
���������R�k�����������W���Ŏ����Ƃ������Ƃ����ł���ȏ�A�����W���̑���������Ƃ���퍐�̎咣�͉���Ӗ��������Ȃ��B |
|
(2) |
�Ȃ��A�O�q�����Ƃ���A�퍐���i�̊O��������R�A�́A���S�R�A���炢������R�k�����������z��������̂ɂ����Ȃ��B���S�R�A����R�k������̎����ɂ��Ă̓g�����X�̏�����p��R��C���_�N�^���X�̌`���Ƃ͖��W�ł��邱�Ƃ͖����ł���B���������āA�O���R�A������Ȃ��ɂ�����炸�A���S�R�A�ɗ���鎥���̐���ɑ傫�ȈႢ�͂Ȃ��B |
|
|
�g�����X�̏�����p�͊����ƍ������鎥���Ƃ̑��ݍ�p�őS�Ă����܂���̂ł��邩��A�������ђʂ��A�����͓r���ŘR��o�������������̌��C����ʂ낤���O���R�A�ɋz������悤���{���I�ȕ����ɂ͉���e���͂Ȃ��B
���������āA�{�����������ɂ����ẮA�O��������R�A�͉���Ӗ���L�����A�P�Ȃ�t�����ɉ߂��Ȃ��̂ł���B |
|
(3) |
�퍐�́A�d�d�^�R�A�A�d�h�^�R�A�A�퍐���i�R�A�y�і_��R�A�ɂ��Ă̎����̔����y�јR��̑���ɂ��ẮA�퍐�������ʁi�R�j�Y�t��P�}�y�ё�Q�}���Q�Ƃ��ꂽ���|�咣���Ă��邪�A�����������̐}�����ł��邱�Ƃ́A�{�������ʑ�P�ɂďq�ׂ��Ƃ���ł���B |
|
|
�X�ɁA�퍐�́A�R�A�̑g���`��ɂ�莥�����z�̎����I���͂Ȃ��Ǝ咣���Ă��邪�A��������ł���B
���ɏq�ׂ��Ƃ���A�{�����������̏o��i�P�X�X�R�N�W���j�ȑO�ɂ����ẮA�d�h�^�R�A�̇T�R�A���퍐�������ʁi�R�j��P�}�L�ڂ̂悤�ɒ������̂͂Ȃ��������Ƃ��O�q�����Ƃ���ł���B
�{�����������ɂ����ẮA���̂悤�ɒ��S�R�A������A���Ȃ킿�A�R�A�f�ʐςɔ�ׂĎ��H���������߂ɁA�j�������ォ�玥�����R�k����Ƃ����A�u�ɒ[�ȘR�k�������ʁv�������邱�ƂɂȂ������̂ł���A�]���̂悤�Ȓ��S�R�A���Z���d�h�^�d�d�^�R�A�ł́A���̂悤�Ȏ����R�k���`�������������͒����������B |
| �@�R |
�u�R�@�{�����������̗v���b�Q�Ƃ̑Δ�v�ɑ��锽�_ |
|
(1) |
�퍐�͍b��P�V�����v���b�Q�̗����ʂ����Ă��Ȃ��|�咣���邪�A����ɂ��Ă̔��_�́A���Ɍ����������ʂS�A�P�O�ŁA�y�ѓ����ʂP�R�łȂ����Q�S�łɂĔ��_�ς݂ł���B�Ȃ��A�퍐�ɂ����čb��P�V���ɂ��ĐV���ɋ�̓I�Ȏ咣��������A�����͓��Y�咣���ɑ��Ώ�����\��ł���B |
|
(2) |
�퍐���i�R�A�̎����̘R��ɂ��ẮA��q�̂Ƃ���ł���B |
| �@�S |
�u�T�@�{�����������̗v���d�P�y�тd�Q�ɂ��āv�ɑ��锽�_ |
|
(1) |
�퍐�́A�퍐���i�ɂ����ẮA���d�ǂ��t���p�l��������O�����ɂ��A�e�ʂ���菜���Ă��A�C���o�[�^��H�͐���ɓ��삷��|�咣����B |
|
(2) |
�������A��L�咣�͉��琔�l�I���t���̂Ȃ��咣�ł���A�C���o�[�^��H���u����v�ɓ��삷��Ƃ����_�ɂ��Ă��A�ǂ̂悤�ȓ���������āu����v�ł��邩���咣���Ă��Ȃ��B |
|
|
�퍐�̏�L�咣�ɑ��ẮA���l�I���t���̂���咣�y�я؋������߂���̂ł���B��̓I�ɂ́A�u���ǂɂ�����d���E�d���������A�d�͂������Ɍv�Z���Ď����悤���߂�B |
|
(3) |
���������A�퍐���i��MP-1010�p�ɐv���ꂽ�g�����X�ł���A���炩���ߕ��d�ǂ��t���p�l���ɐݒu���Ċe�ʂ𗘗p���邱�Ƃ�O���ɓ���Đv����Ă�����̂ł���B |
|
|
���������āA���̉t���p�l�������O�����ꍇ�ɂ́A�\�ߐv�ɓ���Ă����t���p�l���ƕ��d�ǂƂ̊e�ʂ����Ȃ��Ȃ邽�߁A���U���g�����オ��A�u���ǂ��Â��Ȃ�B�K�R�I�ɏ���d�͂���������̂ł����āA����ɂ��������オ�邱�Ƃ͂Ȃ��B |
| �@�T |
�u�U�@�{�����������̗v���d�R�Ƃ̑Δ�v�ɑ��锽�_ |
|
����ɂ��ẮA���U�̂Ƃ���ŁA�ڏq����B |
| ��S |
���U��H�Ƌ��U |
| �@�P |
�퍐�̗��_�̌�� |
|
(1) |
�퍐�́A�퍐���i�̃C���o�[�^��H�͒��U���g����肩�Ȃ荂�����g���ɐݒ肳��Ă��邩��A�{�����������̗v���ɊY�����Ȃ��|�咣����B |
|
(2) |
�������A�퍐�̎咣�́A��������A���U��H�Ƌ��U�ɂ��Ă̌���������ɂ�蓱����Ă�����̂ł���B�ȉ��A����ɂ��ďڏq����B |
| �@�Q |
���U��H�����݂��邱�ƂƂ��ꂪ���U���邱�Ƃ͈قȂ� |
|
(1) |
���U��H�Ƃ��ꂪ���U���邱�� |
|
|
�{�������ɂ����ẮA���̋��U��H�̑��݂��v���ƂȂ��Ă��邪���U��H�����݂��Ă���Ƃ������ƂƁA���U��H�����݂��A���A���ꂪ���U���Ă��邱�ƂƂ͈قȂ�B
�퍐�͋��U��H�����݂��Ă��邱�Ƃ������ăC���o�[�^�̓�����g���������I�ɂ��̋��U�_�œ��삵�Ȃ�������Ȃ����̂��Ƃ�����������Ă���Ǝv����̂ŁA�ȉ��ɂ��̕����ɂ��Đ�����������B |
|
(2) |
�܂��A�퍐�͏������ʁi�R�j�X�łR�s�Ȃ����S�s�ɂ����āu���U��H�͑��݂��Ȃ��v�Əq�ׂȂ�����T�s�ȉ��ł͒��U���g���̋c�_�����Ă���A�������Ă���B |
|
|
���̕����́A�u�퍐���i�ɂ����Ă͒��U��H�͑��݂��邪�A����͋��U���Ă��Ȃ��v�ƕ\�������ׂ��ł���B����͖��炩�ɔ퍐�́A�u���U��H�����݂��邱�Ƃ��A���Ȃ킿���̋��U���g���Ŏ����I�ɃC���o�[�^�����삷�邱�Ƃ������B�v�Ɗ��Ⴂ���Ă��邱�Ƃ�����������̂ł���B�Q�l�܂łɏq�ׂ���̂悤�ɓ��삷���H�̂��Ƃ�����^��H�Ƃ����B�����̗�A�ɊǗp�C���o�[�^��H�͊m���Ɏ���^��H���嗬�ł���A�ꎟ���ɐ݂���ꂽ���U��H�̋��U���g�������Ȃ킿�C���o�[�^�̓�����g�������肷��B |
|
(3) |
���ǁA�퍐�͂��̏]���Z�p�Ɩ{���̋Z�p�Ƃ��������Ă���̂ł���B�����Ă���ɁA�퍐�͏������ʁi�R�j�W�łP�O�s�Ȃ����Q�S�s�ł����l�̌���������ďq�ׂĂ���B |
|
|
�퍐�͂��̋L�q�ŁA�����͔퍐���i�����U���g���œ��삵�Ă�����̂łȂ����Ƃ�F�߂��A�Əq�ׂĂ��邪�A���������A�C�������̓���̑�U���ɂ����ďq�ׂĂ���͔̂퍐���i�ɂ����Ē��U��H�����݂��Ă��邱�Ƃ����Ȃ̂ł���B
���U��H�����݂��A���A���ꂪ���U���Ă��邩�ǂ����������ŏq�ׂĂ���킯�ł͂Ȃ��B�����������U��H�����݂��Ă��邱�ƂƁA���U��H�����݂��A���A���U���Ă��邱�ƂƂ͈Ӗ����S���Ⴄ�̂ł���B
���������āA���̂悤�ɁA���U��H�����݂��Ă��邱�Ƃ݂̂����q�ׂĂ��Ȃ������ɂ����āA�퍐�͑S���I�O��ȃC���o�[�^�̓�����g���ɂ��Ď��₵�Ă����Ƃ������Ƃ́A����͂Ƃ���Ȃ������A�퍐���퍐���i���]���^�̃C���o�[�^��H�̓��쌴�����l�A���U��H�̋��U���g�����C���o�[�^�̓�����g�������肷�鎩��`��H�̌����Ɩ��炩�Ɍ�F�������Ă��邱�Ƃ��������̂ł���B |
|
(4) |
���Ȃ݂ɁA�퍐���i�̏ꍇ�A�C���o�[�^�̓�����g�������߂Ă���̂̓C�������̓����R��
�u�t�P�����̃[���d�����o��H�ɂ��o�͂]�����邽�߂̋��U�d������邽�߂̂��̂ł���B�v�ƋL�q����Ă��镔���ł���A�[���d�����o�@�\�ɂ��C���o�[�^�̓�����g�������肳���B�퍐�̓C���o�[�^�̓�����g�������₵�����̂ł���A���̕����̓���ɂ����Ď��₵�ė���̂��K���ł���A�S���I�O��ȑ�U���ɂ����ăC���o�[�^�̓�����g�������₵�Ă��Ă���̂ł���B |
|
|
���������āA���̂悤�Ȕ퍐�̎���ɑ��ẮA�����������ʂU�ɂē������悤�ɁA���U��H�����݂��Ă���Ƃ������������̂��悤���Ȃ��B |
| �@�R |
MPS�А�IC�ɂ��C���o�[�^������g���̌���@�\ |
|
(1) |
��q�̂悤�ɔ퍐�͒P�ɋ��U��H�����݂��邱�ƂƁA���U��H�����݂��A���A���ꂪ���U���Ă��邱�ƂƂ̋�ʂ����Ă��Ȃ��̂ŁA�Q�l�܂ł�MPS�А�IC�ɂ��C���o�[�^������g���̌���@�\�ɂ��ĊT������B |
|
(2) |
MP-1010�̓��쌴�� |
|
|
MPS�А�IC�AMP-1010�͓����ɂS�̃p���[�g�����W�X�^��L���邪�A���̃p���[�g�����W�X�^��H-Bridge�Ƃ�����H���\�����Ă���B
H-Bridge�̓X�C�b�`�f�q�Ƃ��ē��삵�Ă���A���̃X�C�b�`���O�̃^�C�~���O��ZCS�i�[���E�N���X�E�X�C�b�`�A�����́A�[���E�J�����g�E�X�C�b�`�j�Ƃ����@�\�ŃX�C�b�`���O�̐ؑփ^�C�~���O�������Ă���B
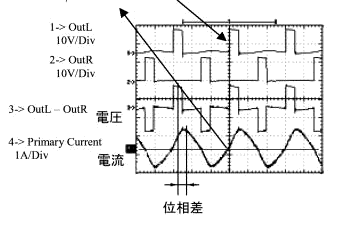
�}2-1 �g�����X�ꎟ�����̓d���Ɠd�� |
����H-Bridge�̓���^�C�~���O�ƃg�����X�ꎟ���ɗ����d���Ƃ̊W��MPS�Ў����T�ł����p����Ǝ��̂悤�ɂȂ�i�}�Q�|�P�j�B
MP-1010��ZCS�����ł͂��̐ؑփ^�C�~���O�����肷�邽�߂Ƀp���[�g�����W�X�^�ɗ����d�����[���ɂȂ邱�Ƃ����o���Đؑւ��s�Ȃ����߁A�p���[�g�����W�X�^�̔��M�����Ȃ��Ȃ�Ƃ������̂ł���B����ZCS�����̓����Ƃ��āA�g�����W�X�^�ɗ����d���̈ʑ���OutL-OutR�̓d���̊�{�g�̈ʑ����������x������B
���̓d���ʑ��ɑ���d���ʑ��x�ꂪ���̂܂܃g�����X�ꎟ�����ɗ^������d���ʑ��ɑ���d���̈ʑ��x��ɂȂ�B
���������āAMP-1010�̓���_�͐}�Q�|�Q�̂悤�ɁA�d���ɑ���d���ʑ���0deg.�����������}�C�i�X���ɂȂ������g���ɂ����ē��삷��̂ł���B
������A�h�~�^���X�O���t�i�}�Q�|�Q��j�Ƃ̊W�Ō���AIC�̓�����g���͒��U���g���Ƃقړ�������������͂��ɒႢ���g���œ��삵�Ă��邱�Ƃ��Ӗ�����B�@ |
|
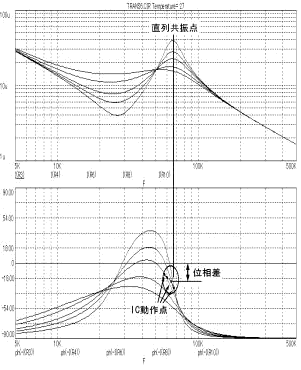
�}2-2 |
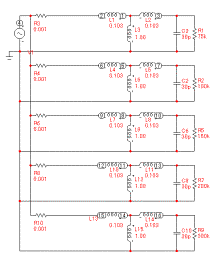
�}2-3
�}2-2�̉�̓��f�� |
|
|
|
���Ƃ��A���U��H�����݂��邱�ƂƁA���̒��U��H�����U���Ă��邱�ƂƂ͈قȂ���̂ł���B
���U���g���͒��U��H�ɂ���Č��肳��A����Ƃ͕ʂ̋@�\�ŃC���o�[�^�̓�����g�������肳��A���̗��҂̎��g�����߂��W�ɂ�����U��H�͋��U����B
�Ȃ��A���́u���U�v�Ƃ������ۂ͒��U�_����ɂ����Ă̂N���錻�ۂł͂Ȃ��B
�퍐�̓C���o�[�^��H�̓�����g���A�܂�͔��U���g���Ƌ��U��H�̋��U���g���Ƃ��킸���ł��قȂ�Ƃ���͋��U�����Ă��Ȃ����̂��Ǝ咣���Ă���悤�ł��邪�A���U���g���Ƌ��U���g���Ƃ��������炢�قȂ��Ă����U��H�͋��U����B���U�̌��ۂɂ͖ڈ��Ƃ��Ĕ��l���Ƃ����T�O�����肱��ɂ��Ă͌�q����B
MP-1010�͏�L�̂Ƃ��蒼�U���g���ɋ߂����g���������I�Ɍ��o���ē�����g�������肷����̂ł��邩��A�C���o�[�^�̓�����g���ƒ��U���g���Ƃ͕K�R�I�ɋ߂����g���ɂȂ�A���U��H�͋��U����̂ł���B
�����ŁA�]�������̃C���o�[�^������ƁA�b��Q�T���؎ʐ^4-1�y��4-2�̃C���o�[�^�̃g�����X�ꎟ���������猩���d���|�d���ʑ��̊W�͂ق�-90deg.�ɋ߂��B�]�������̃C���o�[�^�ɂ����Ă��A���ۂ̃C���o�[�^�̓��쎞�ɂ͂����������דd��������A��������̗͗��͑������P����邪�A�U�����i�㎥�d���j�ƒ�R���i���דd���j�̓d���̃x�N�g���i90�x����Ă���j�����������̂ł͖{���I�ɗ͗���0deg.�ɋ߂Â�����̂ł͂Ȃ��A�͗����������M�̑����������������킯�ł���B�]���̃C���o�[�^��H�ɂ����Ă̓g�����X�ꎟ�����ɗ����㎥�d��������킯�ł͂Ȃ��̂ŁA�㎥�d���ɂ��ꎟ�����̔��M�͖{���I�Ɍ���Ȃ��B
����AMP-1010�̎����ɂ����Ă����炩�Ȃ��Ƃ́A�ꎟ�����ɗ^������d���Ɠd���Ƃ̈ʑ����͔��ɏ��Ȃ��B����́A�퍐���i��MP-1010���g�p����Ă������A�͗��̔��ɗǂ�����_�œ��삵�Ă��邱�Ƃ����̋Z�p�����͎����Ă���A����͂��Ȃ킿�{�������̓����ł���A�͗��̉��P���ʂ�@���ɕ\�����Ă���̂ł���B
�⑫����A�{�������̓����ł��邱�̂悤�ȗ͗��̉��P���ʂ̓g�����X�ꎟ�����̓d���ɑ���d���̃x�N�g�����A���̘R��C���_�N�^���X�ɗ����d���̃x�N�g���Ɠ��ɐڑ����ꂽ�e�ʂɗ����d���̃x�N�g���i���҂�180�x����Ă���j�Ƃ���������邱�Ƃɂ��{���I�Ɉʑ�����0deg.�ɋ߂Â��Ƃ��납�琶������ʂł���A���ꂪ�{�������̒��U�̌��ʂɂ�蔭������͗��̉��P���ʂ̖{�������ł���B
����́A�g�����X�ꎟ�����ɗ����㎥�d�������U�̌��ʂɂ�菭�Ȃ��Ȃ邱�Ƃł���A���̌��ʗ㎥�d���ɂ��ꎟ�����̔��M������̂ł���B
�Ȃ��A���́u�{���̗͗����P�v�ɂ���Ĉꎟ�����̔��M�����邱�Ƃ̓g�����X�̏��^���Ɋ�^���Ă���̂ł���A���̂��Ƃ͎Q�l�܂łɌ�q����B
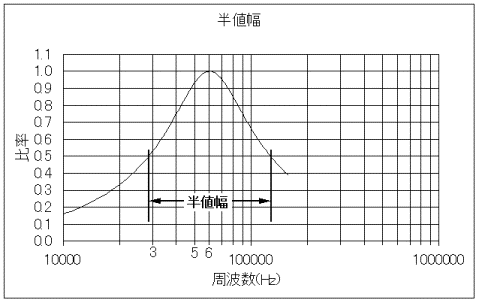
�܂��A���U���g���i���U�_�j�߂����g�債�Ă݂�ƁAIC�̓�����g���̓g�����X�ꎟ���ɗ^������d�͂��傫���Ȃ�A���ɐڑ����ꂽ�u���ǃC���s�[�_���X���Ⴍ�Ȃ�ɂ��������āA�������ɒႭ�Ȃ�X�����͂�����Ɗϑ��ł���i�}�Q�|�S�j�B
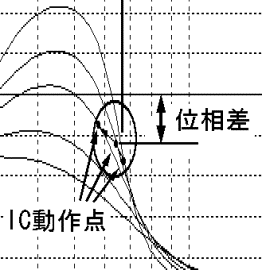
�}2-4 IC����_�t�߂̊g�� |
���́A�u���ǂɗ^������d�͂��傫���Ȃ�i�܂�͊Ǔd����������j�ƂƂ��ɃC���o�[�^�̓�����g�����Ⴍ�Ȃ��Ă����Ƃ��������͍b��P�V���ؐ}�T�̎������ʂƂ�����������̂ł���B
���̂悤�ɁA�퍐���i�Ɏg�p����Ă���MP-1010�͂��̓��쌴���Ƃ��ė͗��̗ǂ����g���������I�ɑI�����ē��삷����̂ł���B
�܂��A���ʂƂ��Ă��̗͗��̗ǂ����g���͒��U���g�����������Ⴂ���g���ɔ�������킯�ł��邩��A����͂Ƃ���Ȃ������A�퍐���i�����U���g�����������Ⴂ���g���Ŗ{�������̏d�v�Ȍ��ʂł���͗��̉��P���ʂ�L���ɗ��p���Ă��邱�Ƃ������B
���������āA�퍐���i�ɂ����ẮA���U���g���ƃC���o�[�^�̓�����g���͋߂��W�ɂȂ�A���U��H�͋��U����̂ł���B
�Ȃ��AMP-1010�̓��쌴���セ�̓�����g���͒��U���g�������킸���ɒႢ���g���ƂȂ邱�Ƃ͉��V����MPS�ЋZ�p�����̒��ɂ����L����Ă���B�iP8Figure5�j
���Ȃ݂ɁA�퍐�͔퍐�������ʁi�R�j�U�ł̂P�s�Ȃ����P�P�s�Œ��U���g�����46KHz�ł���Əq�ׁA�܂��A�C���o�[�^�̓�����g�����62kHz�`��65kHz�ł���Əq�ׂĂ��邪�AMP-1010��IC�̓��쌴����AZCS��L���ɓ�������IC�̔��M��Ⴍ�}���邽�߂ɂ͒��U���g�������C���o�[�^�̓�����g���̕��������ɍ����ȂǂƂ������Ƃ͗L�蓾�Ȃ��B
MP-1010�̓��쌴�����炵�Ĕ퍐���i�̃C���o�[�^�̓�����g������62kHz�`��65kHz�ł���Ȃ�A�퍐���i�ɂ����Ē��U���g����65kHz����������͂��ɍ������g���ɂ���Ƃ������Ƃ��t��IC�̓��쌴���ォ��������邱�Ƃ��ł���킯�ł���B
������b��P�V���S�Ő}�S�ōĊm�F����A�A�h�~�^���X�O���t�ɂ���Ď�����钼�U�_�ƃC���o�[�^�̓�����g���͔��ɋ߂��W�ɂ��邱�Ƃ�������Ă���B
�܂�����ɁA�}�S��3mA��5mA�̃O���t���r����ƁA�Ǔd���������Ȃ�u���ǂ̃C���s�[�_���X���ቺ�����ꍇ�ɂ͒��U���g���ɔ�ׂăC���o�[�^�̓�����g�����Ⴍ�Ȃ��Ă����Ɠ����ɗ͗������ǂ������Ɍ��������Ƃ��Ă���X�����͂�����o�Ă���B
����̓V�~�����[�V�������ʁA�{�������ʐ}�Q�|�Q�Ƃ����ɗǂ���v���A�V�~�����[�V�������f���Ǝ������ʂƂ̈�v�̓V�~�����[�V�������f�������ꂾ���������Ƃ������Ƃ��������̂ł���B
�Ȃ��A�퍐�͌������V�~�����[�V�����ɗp�������f���i�O�[�q������H�j�������P�ɕX��̂��́A�Əq�ׂĂ��邪�A�V�~�����[�V�����Ƃ������̂͂��̂悤�Ȍy�X�������̂ł͂Ȃ��B���f��������������Α�O�҂ɂ��Ӓ�Ɠ����̏؋��\�͂�����ƌ��Ȃ��Ă��ǂ��قǕ��Ր��A�Č����̗ǂ����̂ł���B�����́A�e�d�q���i�̃p�����[�^�i�g�����X�̘R��C���_�N�^���X�A�t���o�b�N���C�g�̊e�ʁj���狁�߂���V�~�����[�V�������ʂƁA����������̑�����ؖ������̎�@�������Ă���A���́A���ꂼ��Ⴄ��@�ŋ��߂����ʂ����ɗǂ���v���邱�Ƃ������Ă���̂ł��邩��A�V�~�����[�V�������f���͐������B�퍐���A���̃V�~�����[�V�������f���Ɉق�������̂ł���A��̓I�Ɏw�E���ꂽ���B
�퍐�́A�����������������i�i������g��54kHz�`58kHz�j�ɔ�ד�����g����������i62kHz�`��65kHz�j�Əq�ׂĂ��邪�A���̏ꍇ�̓A�h�~�^���X�E�ʑ��O���t�y�ђ��U���g���Ƃ��ǂ����g���̍��������֖�7kHz�ړ�����ɉ߂��Ȃ��͂��ł���B
�퍐�͊��Ɍ����������Ă���A�h�~�^���X�|�ʑ������������u�i�b��P�V���ؐ}�R�j�Ɠ������̂����L���Ă��邱�Ƃ��m�F����Ă���i����U���S�ł̐}�T(a)�̑��u�j�̂ŁA�����Ɠ������@�ɂ��������s�Ȃ��Č��ʂ���������ŁA���̌��ʂɗ��r���ċ�̓I�Ȕ��_���s��ꂽ���B |
| �@�S |
�퍐�̒��U���g���̗����̌�� |
|
�Ƃ���ŁA���U���g�������C���o�[�^�̓�����g���̕��������ɍ����|�̔퍐�̎咣�́A�퍐�������ʁi�R�j�T�ł̐}�ɂ����āA���U���g���Ƃ������̂�P�ɊԈႦ�ĕ߂炦�Ă���ɉ߂��Ȃ��B
���U���g���͂ǂ̂悤�Ȋ�{�I�������Q�Ƃ��Ă��e�ʐ����̃��A�N�^���X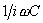 �ƗU�������̃��A�N�^���X �ƗU�������̃��A�N�^���X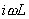 �Ƃ̘a���[���ɂȂ���g���ł���Ə�����Ă���B �Ƃ̘a���[���ɂȂ���g���ł���Ə�����Ă���B
�Ⴆ���U���g�����v�Z���鎮��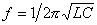 �ł����āA����͂��܂�ɂ���{�I����������ł���B �ł����āA����͂��܂�ɂ���{�I����������ł���B
���̌����̒��ɂ͒�R����R����݂��Ă��Ȃ��B���������āAR�����̑召�ɂ���ċ��U���g�����ς��ȂǂƂ����T�O�͗L�蓾�Ȃ��B�������ʂ̍ő�_�͋��U���g���ł͂Ȃ��̂ł���B
�퍐������������Q���ɂ��܂��q�ׂĂ���u���U�Ƃ͓d���Ɠd�����ő�ɂ�����g���ł���v�Ƃ́A���̑O����悭�ǂ߂A��RR�ƃR���f���TC�ƃC���_�N�^���XL�Ƃ�����ɐڑ����ꂽ�ꍇ�Ɍ��肳���L�q�ł��邱�Ƃ͖��炩�ł���A���҂����܂��܂��̂悤�Ȍ���ɂ��ď������܂Ȃ������ɉ߂��Ȃ��B
�{���̗�ł͒�R����R�͗e�ʐ���C�ƕ���ɐڑ�����Ă���i����V���V��
Figure 4a,4b�j���̂悤�Ȍ`�Ԃ̒��U��H�ɂ��Ă͉���Q���ɂ͉��̐������Ȃ��B
�����ŁA�{���̂悤�ȗe�ʂɕ���ɒ�R���ڑ������ꍇ�̒��U��H�̏ꍇ�A�d���Ɠd�����ǂ̂悤�ȊW�ɂȂ���̂��ĂуV�~�����[�V�����Ŋm�F�����B�i�}�Q�|�T�A�Q�|�U�j |
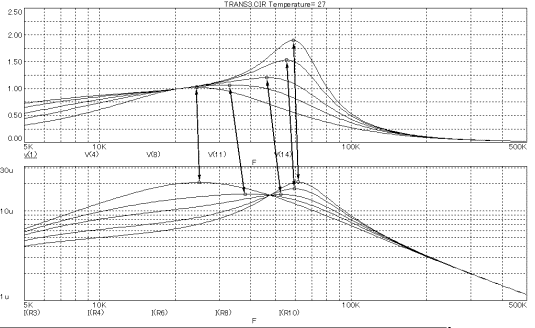
�}2-5 |
|
|
��̐}���d���ł���A���̐}���d���ł���B�퍐�̎咣�̂悤�Ɂu���U�Ƃ͓d���Ɠd�����ő�ɂ�����g���ł���v�Ƃ����̂ł���A�d���̍ő�ƂȂ���g���Ɠd�����ő�ƂȂ���g���Ƃ���Ɉ�v���Ă��Ȃ���Ȃ�Ȃ����A�}�Q�|�T�ł͖��炩�ɂ���Ă��邱�Ƃ��m�F�ł���B
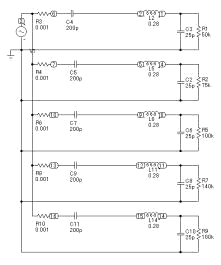
�}2-6 �}2-5�̉�̓��f�� |
���������A�d���̍ő�l�ƂȂ���g���������Ă���U���g���ł���Ƃ���퍐�̎咣�����Ȃ̂ł���B
������ɂ��Ă��A���U���g�������߂鎮��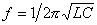 �ł����āA�{���̂悤�ȏ����ό`�������U��H�̏ꍇ�̏������ʒ���͈�ʂɒ��U�_�i���U���g���j�Ƃ͌���Ȃ� �ł����āA�{���̂悤�ȏ����ό`�������U��H�̏ꍇ�̏������ʒ���͈�ʂɒ��U�_�i���U���g���j�Ƃ͌���Ȃ� |
| ��T |
���z�萔���ɂ��� |
| �@�P |
�퍐�̎咣�̌�� |
|
�퍐�͖{�������Z�p�̕��z�萔���Ɋւ��A�����̎咣�y�я؋��ɑ��đS�����_�I�w�i�ⓙ����H�Ƃ��Ă̐��l�I�������Ȃ��A������W�J���Ă���Ǝ咣���A�S�ʓI�ɔ۔F���Ă���B
�������A�����̎咣��؋��́A�����H�w�Ɋւ���m���̂���҂ɂƂ��Ă͎����̂��Ƃł���B
�ȉ��A�ڐ�����B |
| �@�Q |
�����̏؋�����ʓI�ł��邱�� |
|
�퍐�́A��������o����؋����ʓI�ł���ƔF�����Ă��Ȃ��悤�ł��邪�A����߂Ē�ʓI�ł���B |
|
(1) |
�܂��A�퍐��L��C�Ƃɂ��\�������x����H�̂��Ƃɂ��āA��{�I�m���ɑ傫�Ȍ��@�����邱�Ƃ�I�悵�Ă���B |
|
|
�퍐�������ʁi�R�jP10��25�s�ڂȂ���P11��3�s�ڂɁA�u�d�͂���H�̓��̒��������œ`�d����Ƃ����ꍇ�A���̔g���͂T�O�O�Om�ƂȂ�B���ۂɂ͓��̎��ӂ̏�̗U�d���ⓧ�������A�^��̂��������傫�����߁A�d�͂̓`�B���x�͒x���Ȃ�A�g���Ƃ��Ă͒Z���Ȃ邪�A���̊����͂���قǑ傫���͂Ȃ��B�v�A�Əq�ׂ邪�A���̔F���ɂ��������d��ȊԈႢ������B
�����͔퍐�����̂悤�ȊԈႢ��Ƃ��Ȃ��悤�ɗ\�ߍb��P�R�����o���Ă���B���̏��Ђ̂P�O�Q�łɂ͐}�X�|�P�Ƃ��āA�u�f�W�^���E�p���X��H�ɂ͐�nS�`��100nS���炢�܂Łv�̂��̂��g�p�����Ƃ����L�q�����邪�A��������Ă��킩��Ƃ���A�t�F���C�g�R�A�̎���Ɋ����ꂽ�����ɂ͌��Ⴂ�̃C���_�N�^���X���������A�P���ȓ����̏ꍇ�̐M���`�B���x�ɔ�ׂċɓx�̒x�����N����̂ł���B |
|
(2) |
�������̓I�ɁA�퍐���i�����i�ɂ�����������ʂ���v�Z����Ǝ��̂悤�ɂȂ�B |
|
|

�b23�����ʐ^7-1 |
�b��Q�R���̎ʐ^7-1���ēx�Q�Ƃ���B���̏ꍇ�̑��������60kHz�ł���B��������R�C�����Ȃ������̓g�����X��������Ɏ��t����ꂽ���̂ł���B
�܂肱�̎����ł͓�����ɔ�������M���̒x�����ۂ𑨂��Ă�����̂ł���B
�����ŁA����R�C�������炃�܂ł̋�����1.0cm�ł���A���ꂼ��̃R�C���Ɍ��o�����M���̔g�`��2.34�ʕb�x�����Ă���B
�����̂��Ƃ���������ʉ߂���M���̑��x���v�Z����ƁA
�@�@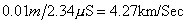
�Ƃ����v�Z���ʂ�������B
���̒l�͌��̓`�d���x�Ɣ�ׂČ��Ⴂ�ɒx�����Ƃ͖��炩�ł���B
�܂��A�g�����A
�@�@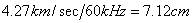
�ƂȂ�B
����ɂ�����A�퍐�̔F���ɍ��킹�ē����̒�������v�Z���Ă݂Ă��A����R�C�������炃�܂ł̊Ԃɑ��݂��銪���̒����́A�P�^�[��������̓����̒�����14mm�A������2000T�Ƃ��Čv�Z����ƁA14�~2000=28000mm��28m�ƂȂ�B�����āA���ꂼ��̃R�C���Ɍ��o�����M���̔g�`��2.34�ʕb�x�����Ă���B�����̂��Ƃ���������ʉ߂���M���̑��x���v�Z����ƁA
�@�@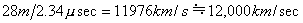
�����ɔg���́A
�@�@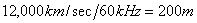
�ƂȂ�B
���ǁA������̎��_���猩�Ă��A���̒l�͌��̓`�d���x�Ɣ�ׂČ��Ⴂ�ɒx�����Ƃ͖��炩�ł���B
������ɂ��Ă��A�g���T�O�O�Om�Ƃ����퍐�̔F���͌��Ⴂ�̌����܂�ł��邱�Ƃ͖��炩�ł���B |
|
(3) |
�܂��퍐�������ʁi�R�j�P�P�ŁA�Q�R�s�ڂ����ł���B |
|
|
�Q�R�s�ڂɁu�����̒����ɑ��Ċ����Ɉ�������T�[�W�̔g���s�x���\���傫���Ƃ��ɓK�p�\�ȓ�����H�ł���v�Ƃ��邪�A�悸�A�O�L�������ƂƓ����悤�ɁA�����̓����̏ꍇ�Ɠ`�d���x���債�ĕς��Ȃ��Ƃ�������ςɊ�Â��Ď咣�����Ă���B
�܂��A������H���u�g���s�x���\���傫���Ƃ��ɓK�p�\�v�Əq�ׂĂ��邪�A����ł͔퍐�͓��Y���Ђ̋L�q�͔���`�̉�͂����Ă���Ƃł��咣�������̂ł��낤���B���Ȃ��Ƃ����Ђ̓��Y�����̋L�q�ł͂ǂ��ɂ��≏���j�ꂽ��ł̉�́i�܂�͔���`��O��ɏq�ׂ邱�ƂƁj�ł���Ƃ͏����Ă��Ȃ����A�����������̏��Ў��́A�����ɂ��T�[�W���������ꍇ�Ƀg�����X��≏�j���邽�߂ɂǂ̂悤�ɕ��z�萔���𗘗p���邩�A�Ƃ������Ƃ𒆐S�ɋL�q���Ă���̂ł���B���̂悤�ɁA���̏��Ђɂ����ݔg���_����ѐi�s�g���_�̍��͐��`��͂�O��ɏq�ׂĂ���̂ł��邩��퍐�̎咣�͎����ł���B
����߂Ċ�b�I�Ȃ��Ƃ��q�ׂ邪�A���`��͂Ƃ͓d���������Ⴂ�ɂ�����炸�A������\��������i�i�܂�̓C���_�N�^���X�A�R���f���T�A��R�j�̃p�����[�^���ω����Ȃ��ꍇ�̉�͂̂��Ƃł���B�d���������Ⴂ�ɂ�����炸�A�i�s�g�̑��x�ɂ���ݔg�̔��������ɂ��ω��͂Ȃ��B |
|
(4) |
�܂��A�퍐�͔퍐���i�y�ё������i�̓����ɕ��ՓI�ɕ��z�萔���������Ă��邱�Ƃ�ے肷�邽�߂ɁA�����̎������������ʂ�S���������悤�Ƃ��Ă���B |
|
|
�Ăэb��Q�R�����ʐ^7-2���Q�Ƃ���B
�ʐ^7-2�͑������i�̓�����ɔ�������i�s�g���ݔg���ϑ��������̂ł���B���̂悤�ɓ�����ɐ݂�����������R�C�����Ȃ������̊Ԃɓd����ʑ��̈Ⴂ�������邱�Ǝ��́A���z�萔���̏؋��Ȃ̂ł���B
�����̎����R�ꂪ�����̕��z�萔���x����H�ɂ����̂ł��邱�Ƃ́A�b��R�R���R�R�ł̑�2-26�}�Ƃ̕��������Ă݂�Ζ��炩�ł���B
�����ŁAZo�Ƃ͓`���H�̓����C���s�[�_���X�ł���AZr�Ƃ͕��ׂ̃C���s�[�_���X�ł���BZo��Zr����������Γ`���H�ɂ͂��˂�͔������Ȃ��B�i�@�j�Ƃ��낪�AZo��Zr�Ƃ���v���Ȃ��Ɠ`���H�ɂ͂��˂肪��������̂ł���B�i�A����чB�j
�����̌��ۂ̓A�}�`���A�����△���Z�p�]���҂̊Ԃł�SWR�i��ݔg��j�Ƃ��Ĉ�ʂɒm���Ă�����̂ł���B
�{���̃g�����X�̓�����ɂ�����Ɠ������ۂ��������Ă���B |
|
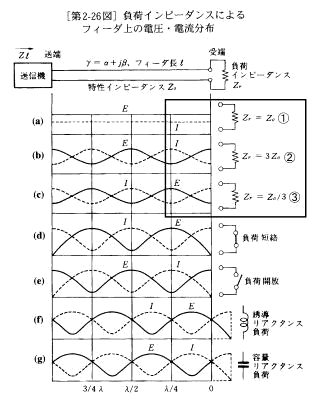
�}3-1
�b��R�R���ؑ�2-26�} |
|
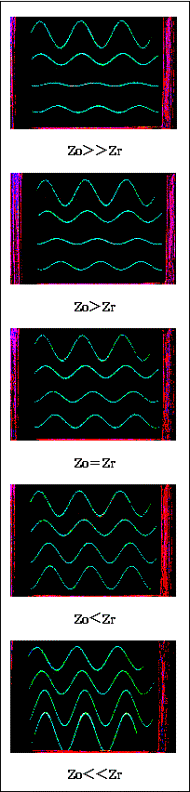
�b��Q�R�����
�ʐ^7-2 |
|
|
|
�}�R�|�P�Ɛ}7-2�̑Δ���ڍׂɎ��������̂��}�R�|�Q�ł���B |
|
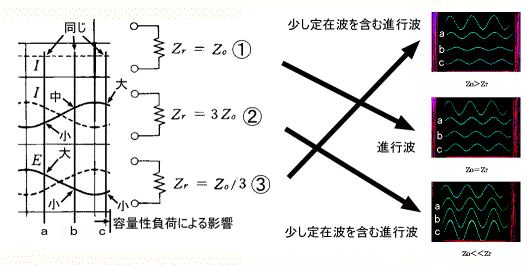
�}3-2 |
|
|
|
���������A������ɕ��z�萔���`���H�ƑS�������悤�Ȓ�ݔg��i�s�g���������Ă��邱�Ƃ͖��炩�ł���B |
|
(5) |
�܂��A�퍐�͌����������؋����ʓI�ł͂Ȃ��Ɣ۔F���邪�A�b��P�V���̎������ʐ}�P�O�i�}�S�ƊԈႢ������̂Œ�������j�͖��炩�Ȓ�ʓI�����R��������Ă���̂ōĂш��p����B |
|
|
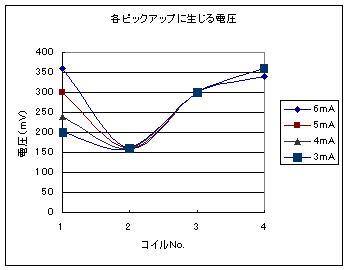
�b��P�V�����}10�d������������ |
�������o�R�C���Q�C�R�C�S�i�ʐ^7-1�ł�a,b,c�ɊY���j�̓d���ɖ��炩�ɒ�ʓI�ȈႢ�������Ă���iL2=160mV�AL3=300mV�AL4=340�`360mV�j�B
��̓I�ȓd���̍��͂��Ȃ킿���ԓI�ɕω����鎥���{���̍��ł�������ォ��R��鎥���̖{�����Ӗ����AL2��L3�y��L3��L4�̊Ԃ���R��Ă��鎥���̗ʂɔ�Ⴗ��킯�ł���B�܂�����ɁA�����͍b��Q�R���R�łȂ����S�łɂ����āA�����������˂�̑傫�����甽�˔g�䗦�iSWR�j�܂ŎZ�o���Ă���B���˔g�䗦�͖�35���ł���B
�܂��A���������i�����悻L2�̂�����j�Ɋѓ����Ă���厥���̗ʂ͔��˔g�̉e���ɂ�菭���킩��ɂ����Ȃ��Ă��邪�A����ł����Ȃ��Ƃ�150mV�������͑����B�i��ݔg�̉e�����Ȃ�������炭250mV�������x�ł��낤�j
����ɔ�ׂđa�������ł���L2��L3�Ƃ̊ԂŘR��鎥���ʂ�140mV�����A����сAL3��L4�Ƃ̊ԂŘR��鎥���ʂ͂��悻50mV�����ł���B
�퍐�͂��̂悤�ȋ�̓I�Ȑ��l����ʓI�łȂ��Ƃ���Ȃ�Ή��������Ē�ʓI���l�Ƃ����̂ł��낤���B���Ɍ����ɂ����āA��q����悤�ȑ�����@�y�ѐ��l���������̂ł��邩��A�퍐�ɂ����Ă���̓I�Ȏ��Ƒ���l�������Ĕ��_���ꂽ���B |
| ��U |
�����W���ɂ��� |
| �@�P |
�퍐�̌����W���̗��_�̌�� |
|
�퍐�́A�����W���������āA�퍐���i�̊O��������R�A���t�����ł͂Ȃ��Ƃ��A�퍐���i�͖{�������ɂ�����u�R�k�����^�v�ł͂Ȃ��|�咣����B
���ɁA�����������ʂS�A�u��T�@�����W���ɂ��āv�i�S�R�ňȉ��j�ɂ����āA�����W�����R�k�����Ƃ͉���W�̂Ȃ��|���_�������A�퍐�������W���ɂ��Ď咣���Ă��邽�߁A�ēx�A����ɑ����_����B |
| �@�Q |
�����W���͎����R��̎w�W�ł͂Ȃ����ƁB |
|
(1) |
�����W���͎����R��̎w�W�ł͂Ȃ��B���ȃC���_�N�^���X�Ƃi�h�r�R��C���_�N�^���X�̔䂩�狁�߂���W���ł���B |
|
|
�g�����X�ɂ�����悭�������Ƃ��āA�����W�����Ⴂ�Ǝ������R��₷���Ƃ������M������B |
|
(2) |
�܂��A�������ȃC���_�N�^���X�l��L����g�����X���m�Ŕ�r�����ꍇ�A�����W�����P�ɋ߂��قǎ����R��͏��Ȃ��Ƃ������Ƃ́A�������B�Ȃ��Ȃ�A�����W�����P�ɋ߂��قǁA�i�h�r�R��C���_�N�^���X�i�ꎟ����Z�����Čv�������ꍇ�ɓ��Ŋϑ������c���C���_�N�^���X�A�܂�͒Z���c���C���_�N�^���X�j�̒l���������Ȃ邩��ł���B |
|
|
��ʂɂ����u�����W�����������玥���R��͏��Ȃ��v�Ƃ�����ʔO�͂������琶�܂�Ă���B |
|
(3) |
�Ƃ��낪����ŁA�����i�h�r�R��C���_�N�^���X�l��L����g�����X���m�Ŕ�r�����ꍇ�A�����W�����P�ɋ߂��قǎ����R�ꂪ���Ȃ����Ƃ����A���ꂪ�����͂Ȃ�Ȃ��B�Ȃ��Ȃ�Δ퍐���������ʁi�R�j�P�U�ł̂Q�T�s�ڂȂ����P�V�ł�3�s�ڂɔF�߂�悤�ɘR�ꎥ���ʂƕ��דd���̑傫���Ƃ��֘A�t����̂��R��C���_�N�^���X������ł���B���Ȃ킿�A�R��C���_�N�^���X�����܂��ĕ��דd�������܂�Ύ����R��̐�Ηʂ͌��܂��Ă��܂��B�R��C���_�N�^���X�l�����������R��̎w�W�Ȃ̂ł���B |
|
|
�����Ŗ��炩�Ȃ��Ƃ͎��ȃC���_�N�^���X�l�͎����R��Ƃ͊W�Ȃ��B���������Č����W���������R��Ƃ͖��W�Ȃ̂ł���B
�܂��A�퍐�́A�������ʁi�R�j�P�U�ł̂Q�T�s�ڂȂ����P�V�ł�3�s�ڂ̋L�q�������Č����̎咣�ł���A�u�{�����������Ƃ̊W�ɂ����Ă�Ls�i�i�h�r�R��C���_�N�^���X�j�݂̂��d�v�ł����āALo�i���ȃC���_�N�^���X�j�͊W�Ȃ��B�i�����j���������Č����W���͖{�������ɂ͊W�Ȃ����l�ł���B�v�Ƃ������Ƃ�F�߂Ă��܂��Ă��邱�ƂɂȂ�B�퍐�ƌ����Ƃ̊ԂɌ����W���Ɋւ�����߂̑����͎c�邪�A�R��C���_�N�^���X�l�Ƃ����𗬂��d�����R�ꎥ���̐�Ηʂ����߂���̂��Ƃ����_�ł͔F������v���Ă���B |
|
(4) |
�g�����X���R�k�������Ƃ��Ďg���Ă��邩�ۂ��͂��̃g�����X�̎��R��C���_�N�^���X�l�����ׂ̃C���s�[�_���X�Ƃ̊W�ʼne���������悤�Ȓl���ǂ����Ō��܂�B |
|
|
��ʘ_�Ō����A����g�����X���R�k�����^�g�����X�ł��邩�ǂ����̓g�����X�P�̂Ō��߂邱�Ƃ͂ł��Ȃ��B
���ׂƂ̊W�ŘR�k�������������ł���悤�Ȏg�����������ꍇ�A���̃g�����X�͔�R�k�����^�g�����X�i���H�^�g�����X�j�ƂȂ�A���ׂƂ̊W�Ŗ����ł��Ȃ��悤�Ȏg�����������ꍇ�A�R�k�����^�g�����X�ƂȂ�B
����A�{���ɂ����ẮA��̓I�ɂ͔퍐���i��Ls������U���ɂ���256.7mH�i�퍐�\�LLts�j�ł���B�Ȃ��ALs�i�퍐�W�LLts�j�Ƃ�JIS�R��C���_�N�^���X�ł���B����͑���l��65KHz�ł��邪�A���z�e�ʂ̉e���͎Ă��Ȃ��̂Œl�͐M�p�ł���B����A���ȃC���_�N�^���XLo�i�퍐�\�LLs�j�l�͕��z�e�ʂ̉e�����Ă��邽�ߐM�p�ł��Ȃ��B
�Ȃ��A���i�ɒ�`����ƘR��C���_�N�^���X�̒l�ɂ͂i�h�r�ɂ����̂Ɠd�C�w��ɂ����̂Ƃ�����A�����̐��l�̊Ԃɂ͖�Q�{�̍�������B�����������ʁi�T�j�Ŏ������悤�ɁA�d�C�w��R��C���_�N�^���X�ł͘R��C���_�N�^���X���ꎟ���Ɠ��ɐܔ����Ă��ꂼ���R��C���_�N�^���XLe�Ƃ��Ă���̂ɑ��AJIS�R��C���_�N�^���XLs�ł�Le���ꎟ�������͓��ɏW�����āi���Z���āj�������Ă��邽�߂ł���B
���̒l������g��65kHz�ɂ�����i�h�r�R��C���_�N�^���X�̃��A�N�^���X���v�Z����ƁA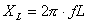 �̌v�Z�����104.8k���Ƌ��߂���B �̌v�Z�����104.8k���Ƌ��߂���B
�����ŁA�퍐��AMBIT�Ђ���m�F������A�Ɋǂ̒�R�l��100k�����x�ł���Ǝ咣���Ă������߁i�퍐�������ʁi�R�j4�ł�10�s�ځj�A���̒l�ƌ���ׂĂ݂�ƁA�R��C���_�N�^���X�ƕ��ג�R�͂قړ����l���Ƃ�A�e���������l�ł���Ɗm�F�����B�����͑����i�̉t���p�l���̊e�ʂ�8pF�Ƒ��肵���B�C���̓���ɂ�����R���f���T��15pF�ł���B�퍐���i�����i�̃g�����X�̈ꎟ�������z�e�ʂ�2.7pF�ł���B�����̍��v�e�ʂ͖�25pF�ƂȂ�̂ŁA65kHz�ɂ����郊�A�N�^���X���v�Z����ƁA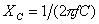 �̌v�Z�����97.9k���Ƌ��܂�B���̒l�̓C���o�[�^������g��65kHz�ɂ����Ă̋��U��Ԃ������A�i�h�r�R��C���_�N�^���X256.7mH�Ɖe���������l�ł���ƌ�����B �̌v�Z�����97.9k���Ƌ��܂�B���̒l�̓C���o�[�^������g��65kHz�ɂ����Ă̋��U��Ԃ������A�i�h�r�R��C���_�N�^���X256.7mH�Ɖe���������l�ł���ƌ�����B
����āA�퍐�̎咣�ł���퍐���i�Ɏg���Ă���g�����X�͔�R�k�����^�ł���Ƃ������ƁA�y�ы��U��H�͑��݂��Ȃ��Ƃ������Ƃ͔۔F����B�퍐���i�́A�R�k�����^�ł���A���A���U��H�����݂��ċ��U������̂ł���B |
|
(5) |
�퍐�������ʁi�R�j�P�V�ł̂R�s�Ȃ����T�s�̋L�q�ɂ��A��ʘ_�Ƃ��āA�g�����X���R�k�����^�Ƃ��Ďg����̂��A��R�k�����^�i�܂�͕��H�^�j�Ƃ��Ďg����̂��A���i�o�בO�Ƀg�����X�P�̂Ō��܂��Ă�����̂ł͂Ȃ��Ƃ��������̎咣�ɂ͈٘_��������̂Ɛ��������B |
|
|
�����āA�퍐�͘R�k�����^���ۂ������̔��f�̂��߂Ɍ����W����ڈ��ɂ���ׂ����Ǝ咣���Ă���B
�������A���Ȃ��Ƃ��A�퍐���i�Ɍ���ΘR��C���_�N�^���X�̃��A�N�^���X�ƕ��ׂ̃C���s�[�_���X�Ƃ̊W�͍ŏ����疾�m�ł���B�Ȃ��Ȃ�A�퍐���i�͂c���k�k�А��t���m�[�g�p�\�R���̃C���o�[�^�p�Ɏg����g�����X�Ƃ��āA�J�X�^���i�Ƃ��Ē�������o�ׂ���Ă�����̂�����ł���B���Ȃ킿�A�ΏۂƂ��镉�ׂɑ����p�i�ł���B
�O�L�̌v�Z���ʂ�����A�C���o�[�^������g���ɂ�����R��C���_�N�^���X�̃��A�N�^���X����100K���ł���A14�C���`�t���p�l���̕��ז�100K���ɍ��킹�č�荞�܂�Ă��邱�Ƃ����炩�ƂȂ��Ă���B
����āA�퍐���i�͘R�k�����^�g�����X�Ƃ��ďo�ׂ��Ă���̂ł���B |
|
(6) |
�܂��A�g�����X�����ׂƂ̊W�Ŏg�����ɂ���ĘR�k�����^�g�����X�Ƃ��ĐU��������R�k�����^�g�����X�i���H�g�����X�j�Ƃ��ĐU�������ɂ��āA�b��P�U���̎��؎�������(1)�̇A�y��(2)�̇A�̎ʐ^�́A�d��Ȍ��ʂ𑨂��Ă���B |
|
|
�g�����X�͍b��P�U���̎��؎�������(1)�̇A�y��(2)�̇A�̎ʐ^�Ŏ�����Ă���悤�ɁA�R��C���_�N�^���X�ɔ�ׂĕ��ׂ̃C���s�[�_���X��e�ʂ̃��A�N�^���X���߂����ۂ��i�܂�͋��U���g���œ��삳���Ă��邩�ۂ��j�ɂ�苓�����ς��B
�R��C���_�N�^���X�̃��A�N�^���X�Ɨe�ʂ̃��A�N�^���X�y�ѕ��ׂ̃C���s�[�_���X�Ƃ̊W���߂��ƃg�����X�̘R�ꎥ�����ɒ[�ɑ����Ȃ�A����ɖ{�������̓����ł��������̎����R�ꂪ�ϑ������B���Ȃ킿�A�g�����X�͖{�������̘R�k�����^�g�����X�Ƃ��ē��삷��̂ł���B
����A�R��C���_�N�^���X�̃��A�N�^���X�ɔ�ׂĕ��ׂ̃C���s�[�_���X��e�ʂ̃��A�N�^���X�Ƃ̊W�������i�܂�͋��U�����Ă��Ȃ��j�ƃg�����X�͔�R�k�����^�i���H�^�j�g�����X�Ƃ��ċ�������B
���Ȃ킿�A�R�k�����^�g�����X�ł��邩�ۂ��͘R��C���_�N�^���X�Ƃ���ɐڑ����镉�ׂƂ̊W�Ō��܂�Ƃ������Ƃ����R�Ȋw���ۂ̔����Ƃ��Ď�����Ă���̂ł���B |
| �@�R |
�ɒ[�ȘR�k�����̈Ӗ� |
|
(1) |
�퍐�́A�{�����������ɂ����u�ɒ[�ȘR�k�����v�Ɋւ��āA�]���̑傫�ȘR�k�������ɔ䂵�Ă���ɑ傫�ȘR�k�������̂��Ƃł���Ƃ��Č����W���Ƃ̊W�Ŏ咣���q�ׂ邪�A���̉��߂͌��ł���B
�܂��A�u�ɒ[�ȘR�k�����v�Ƃ��������ł��邪�A�{���������ɂ́y0010�z�u�����g�����X�̌`���_��̘R�k�����g�����X�ɂ��邱�Ƃɂ��ɒ[�ȘR�k�������ʂ���������ƁA�ꎟ�����ߖT�̓����͘R�k�����g�����X�Ƃ��Ă̌��ʂ�L���A�����Ɉꎟ�������牓�[�̓����̓`���[�N�R�C���Ƃ��Ă̌��ʂ�L����v�ƋL�ڂ���Ă�����̂ł���A�����P�P�N���萿����U�O�O�V�S���W�ł̂Q�s�Ȃ����R�s�ɏq�ׂ��Ă���悤�Ɂu�u�V���C���_�N�^���ʁv�i��̓I�ɂ́u�ɒ[�ȘR�k�������ʁv�j�v�Ƃ����Ӗ��ł���i����Q���j�B���Ȃ킿�A�{�����������̐������Ō����Ƃ���́A�����̈ꎟ�������痣�ꂽ�������a�������ƂȂ�A�Ƃ����̂��V���C���_�N�^���ʂł���A�u�ɒ[�ȘR�k�������ʁv�ł���B
���������āA���́u�ɒ[�ȘR�k�������ʁv�������]���̘R�k�����^�g�����X�Ɩ{���̘R�k�����^�g�����X�̎����R��Ƃ̈Ⴂ���w���Ă��邱�ƂɂȂ�B |
|
(2) |
���ɔ퍐���咣����悤�ɁA�u�ɒ[�ȘR�k�������v���]���̘R�k�����������P���ɘR�k���������傫�����́A�܂�͔퍐���咣����悤�Ɍ����W�����Ⴂ���̂ł���Ɖ��߂��悤�Ƃ���ƁA�������ʁi�R�j�P�W�ł̂Q�P�s�Ȃ����Q�S�s�ň��p���ďq�ׂ�悤�ɁA�]���^�ł����Ă������W����0.01�̃g�����X�����Ɏ��p������Ă���@�Ƃ������̂�����A�{�������͐������Ȃ��B |
|
|
����āA�����W���̑召���{���ɂ����u�ɒ[�ȘR�k�������v�����߂���̂ł͂Ȃ����Ƃ͈�ڗđR�ł���B |
| �@�S |
�i�h�r�R��C���_�N�^���X�ɂ��� |
|
(1) |
���q�̂Ƃ���A�{�������Z�p�ɂƂ��ďd�v�Ȃ̂͂i�h�r�R��C���_�N�^���XLs�̒l�ł����Ď��ȃC���_�N�^���XLo�̒l�ł͂Ȃ��BLs�͖{���������ɋL�ڂ��钼�U���\������d�v�ȃp�����[�^�ł������ALo�̒l�͕��U���\������p�����[�^�Ȃ̂ł��邩��{�����ɂ����Ă͋Z�p�I�ɂ��܂�Ӗ��������Ȃ��B |
|
|
�X�ɁA�{�����������ɂ�Lo�̂��Ƃ����U�̂��Ƃ���؋L�ڂ��Ă��Ȃ��̂ł���B������Lo�y�ѕ��U�̂��Ƃ��L�ڂ���Ă��Ȃ����Ƃɂ��Ă͓�̈Ӗ������B�悸�A�Z�p�I�ɊW���Ȃ�����L�ڂ��Ȃ������̂ł���BLo��Ls����v�Z����錋���W���͖{�����������ォ����{�������Ƃ͊W���Ȃ��̂ł���B���������āA�����̂�����̗��R���猩�Ă������W���Ɩ{�������Z�p�Ƃ͉��̊W���Ȃ����Ƃ͖����ł���B |
|
(2) |
��L�ŏq�ׂĂ����悤�ɁA�{�����������ɏq�ׂ�R�k�����Ƃ͒��U�ɊW������̂ł���B |
|
|
�����ŏq�ׂ�u�ɒ[�ȘR�k�����v�Ƃ́A��̓I�ɂ͂��̒l�̑召�Ƃ͂�����\������i�h�r�R��C���_�N�^���X�̑召�̂��Ƃ��Ӗ�����B
�i�h�r�R��C���_�N�^���X�����ɑ��ĊW���邩�Ƃ����A�O�q�����悤�ɕ��ׂƂȂ�u���ǃC���s�[�_���X�Ɣ�r���ĊW����Ƃ����Ӗ��ł���B |
|
(3) |
�����ŁAJIS�R��C���_�N�^���X�̑召�ƌu���ǃC���s�[�_���X�ƂɊւ�����j�I���ڂɂ��Đ�������B |
|
|
�ł����j�̌Â��]���^�C���o�[�^��H�Ƃ͍b��Q�T���؎ʐ^4-1�Ȃ���4-2�Ŏ������C���o�[�^��H�̂��Ƃł���B
���̃C���o�[�^��H�ɂ����Ďg���Ă���g�����X�̂i�h�r�R��C���_�N�^���XLs�𑪒肷���110mH�ƂȂ�B�܂��A�C���o�[�^�̓�����g����21kHz�A���ׂƂȂ�u���ǂ̃C���s�[�_���X�͎��p�Ǔd����5mA�ɂ�����55.2k���ł���B����Ls�l�ƃC���o�[�^������g�����炻�̎��g���ɂ�����Ls�̃��A�N�^���X�l�����߂�ƁA14k���Ƃ����l��������B
���̒l�ƕ��ׂ̗�A�Ɋǂ̃C���s�[�_���X���r����Ɩ�S�{�i3.8�{�j���J��������B���������āA���̃C���o�[�^��H�͘R��C���_�N�^���X�̑��݂����Ďg���Ă���B
�܂��A���U���g���ƃC���o�[�^��H�̓�����g���Ƃ̊W�ɂ����Ă��b��Q�T���ؐ}4-1����13.4�{���̊J�������邱�Ƃ��킩��A���̃C���o�[�^��H�͒��U���g���̑��݂��������Ďg���Ă���B���Ȃ킿�A�C���o�[�^��H�ɂ����Ă�Ls�̑��݂͈�ؖ�������Ă���̂ł��邩��A���̃g�����X�͔�R�k�����^�g�����X�i���H�^�g�����X�j�Ƃ��Ďg���Ă���̂ł���B
���ɁA�{�����Z�p�Ə]���^�C���o�[�^��H�Ƃ̒��ԓI�ȋZ�p�Ƃ��āA�P�X�X�T�N�ȍ~�A�����Ɏg���n�߂��Z�p������A���ꂪ������R�{���U�^�Z�p�ƌĂ����̂ł���B�i�b��T���Q�R�łȂ����Q�S�Łj
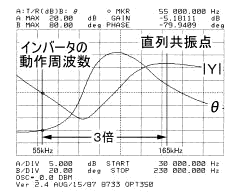
�}4-1 �R�{���U |
���̋Z�p�Ɋ�Â��C���o�[�^��H�̃A�h�~�^���X�E�ʑ������𑪒肵�����̂��}�S�|�P�ł���B���U���g���ƃC���o�[�^��H�̓�����g���Ƃ̊W�͂��傤�ǂR�{�ł���B���̃C���o�[�^��H�̏ꍇ�A�g���Ă���g�����X��Ls�l��55.7mH�ł���A�C���o�[�^�̓�����g��55kHz�ɂ�����Ls�̃��A�N�^���X�l��19.2k���ł���B���̃C���o�[�^��H�ɂ����Ă̓g�����X�̘R��C���_�N�^���X��ϋɓI�ɂR�{�����g�̋��U�ɗ��p���Ă���A�g�����X�̎g�����Ƃ��Ă͘R�k�����^�g�����X�Ƃ��ė��p���Ă��邱�ƂɂȂ�B�����Ď��オ����ɐi���̂��{���̃C���o�[�^��H�ł���B
�Ȃ��A�{���̔����͂P�X�X�R�N�ɍs���Ă��邪�A�����ɕ��y���n�߂��̂͂P�X�X�X�N�ȍ~�ł���B����́A��pIC�̕��y�ƊW������A����͍b��S���؋y�эb��T���ؖ`���ŏq�ׂĂ���B
�i�h�r�R��C���_�N�^���X�̒l��257mH�i�퍐���i�j�ƂȂ�A�C���o�[�^������g���ɂ����郊�A�N�^���X�͗�A�Ɋǂ̃C���s�[�_���X�Ƃقړ������Ȃ����B
�C���o�[�^�̓�����g���ƒ��U���g���Ƃ̊W��1�{�Ȃ����͂Q�{�ȉ��ł���B���Ȃ킿�A�g�����X�̘R��C���_�N�^���X��ϋɓI�ɗ��p���A��{�g�ɂ����Ă����U�𗘗p���Ă���̂ł���B
�����̊W���ꗗ�\�ɂ���Ǝ��̂悤�ɂȂ�B
|
�R��C���_�N
�^���XmH |
�C���o�[�^
���g��kHz |
���A�N�^���X
k�� |
�ǒ�Rk��
(5mA) |
�� |
| �]���^ |
110 |
21 |
14.5 |
55.2 |
3.803 |
| �R�{���U |
55.7 |
55 |
19.2 |
75 |
3.896 |
�{
�� |
�����i�P |
311 |
54 |
105.5 |
110 |
1.042 |
| �����i�Q |
286 |
61.5 |
110.5 |
120 |
1.086 |
| �퍐���i |
257 |
62 |
100.1 |
100 |
0.99 |
�]���^�y�тR�{���U�^�ɔ�ׁA�{���̃C���o�[�^��H�Ɏg���Ă���g�����X��Ls�l�����M�I�ɑ傫���͈̂�ڗđR�ł���A���ꂪ�u�ɒ[�ȘR�k�����v�̎����Ӗ��̈�ł���Ɠ����ɂ���͗V���C���_�N�^���ʁi�{�����������ɂ����A�ɒ[�ȘR�k�������ʁj���������₷�������ł�����B |
|
(4) |
�ȏ�q�ׂ��悤�ɁA�{�����������Ƃ̊W�ɂ����āA�u�ɒ[�ȘR�k�����v�Ƃ͕��׃C���s�[�_���X�ɑ���Ls�i�̃��A�N�^���X�j�̑傫���A�����͗V���C���_�N�^���ʂ��̂��̂�\���Ƃ����Ӗ��ł���B |
|
|
Ls�̑傫���A�V���C���_�N�^���ʁA�����ꂵ�Ă��A�ɒ[�ȘR�k������/�ɒ[�ȘR�k�������ʂ̉��߂̓g�����X�̌����W���Ƃ͖��W�Ȃ��̂ƂȂ�͖̂��炩�ł���B |
|
(5) |
�⑫�܂łɏq�ׂ邪�A�퍐�������܂ł��{�������Z�p�������W���Ɗ֘A�t���Ď咣�𑱂���̂ł���A���̓�̃V�~�����[�V�����O���t�����Č����W���ƒ��U���g���Ƃ̊W�ɂ��Ĕ��f����ׂ��ł���B |
|
|
����U�����퍐���i�Ɏg���Ă���g�����X�̌����W����0.962�Ƃ��ALo��Ls�iJIS
C 5321�\�L�ɓ���j�����ꂼ��3,456mH�A256.7mH�Ƃ���B
��������d�C�w��R��C���_�N�^���XLe�Ƒ��݃C���_�N�^���XM�����߂�ƁA���ꂼ��130.8mH�A3325mH�Ƌ��܂�B
����ɂ��V�~�����[�V�������s�������̂��}�S�|�Q�ł���B
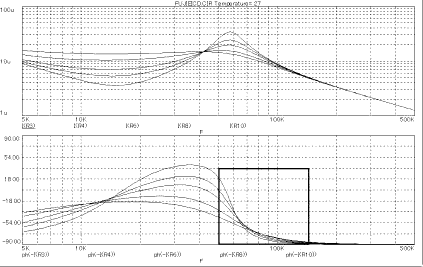
�}4-2 �����W��0.962 |
���ɁA�퍐���i�Ƃقړ��`��ł���A�퍐�֘A���FDK�Ђ̃g�����X�̎����i�b��R�X���j�����ƂɌ����W����0.849�i�R�A�`���ꂩ���p�r�����Ȃ�Α傫���͈قȂ�Ȃ��j�ƌ��ς����āA���ȃC���_�N�^���XLo��917mH�Ƃ��A���̒l����d�C�w��R��C���_�N�^���XLe�Ƒ��݃C���_�N�^���XM�����߂�ƁA���ꂼ��138.9mH�A778mH�Ƌ��܂�B
����ɂ��V�~�����[�V�������s�������̂��}�S�|�R�ł���B
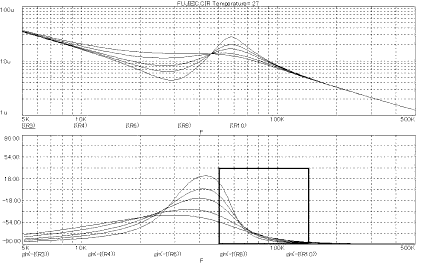
�}4-3 �����W��0.849 |
�����ŁA�����̐}�̒��U�_�t�߁i���ň͂��������j�ɂ��������������ׂČ���ƁA�ǂ�����قƂ�Ǖς�肪�Ȃ����Ƃ��킩��B
������Ls�̒l���Ƃ��Č����W���݂̂�ς��Ă݂����̂ł���B
���������āA���̂悤�ȃV�~�����[�V�������ʂɂ���Ă��A�{�������Z�p�ƌ����W���Ƃ͖��W�ł���Ƃ������Ƃ����炩�ɂȂ�̂ł���B |
| ��V |
���̑��̗��_�I�E�Z�p�I�Ȕ��_ |
| �@�P |
���U���ۂ̋y�Ԕ͈͔��l���ɂ��� |
|
(1) |
�퍐�͋��U��H�����݂��邱�ƂƋ��U��H�����݂��A���A���̋��U��H�����U���邱�ƂƂ̈Ⴂ�������ł��Ă��Ȃ��̂��A�C���o�[�^�̓�����g�������U���g���܂�͋��U�_�œ��삵�Ă��Ȃ����肻��͋��U���Ă���Ƃ͔F�߂Ȃ��Ǝ咣���Ă���̂������܈���m�ł͂Ȃ��̂ňȉ��ɋ��U���ۂɂ������ʘ_���q�ׂ�B |
|
(2) |
���U���ۂƂ͋��U��H�����݂��A���̋��U��H�̋��U���g���ƁA�O������^����ꂽ�M���̎��g���Ƃ��߂��W�ɂ�����U���ۂ���������B |
|
|
�{���̃C���o�[�^��H�̏ꍇ�A�O������^����ꂽ�M���Ƃ͂��Ȃ킿�C���o�[�^��H�̓�����g���i���U���g���j�ł���B |
|
(3) |
����ł́A���U��H�̋��U���g���ƊO������^����ꂽ�M���̎��g���Ƃ��ǂꂾ���߂��W�ɂ�����U���ۂ������邩�ɂ��Ă͈�̖ڈ��Ƃ��Ĕ��l���Ƃ����T�O������B |
|
|
�b��S�O���ɕ����̈��p�������B
���l���Ƃ͋��U�̌��ʂ̒��_�ɔ�ׂēd�����邢�͓d���̎���̒l�������ɂȂ���g���ł���B
�����ŁA�b��S�O���Q�R�R�ł�8.37���ɂ��������āA���l�������߂Ă݂����̂��}�T�|�P�ł���B
�Ȃ��A8.37���͈ꕔ��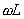 �Ƃ����L�ڂ����邪�A����� �Ƃ����L�ڂ����邪�A�����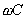 �̌�A�ł���̂ŏ��Џo�ŎЂɊm�F���A�������邱�Ƃ̊m�F���B �̌�A�ł���̂ŏ��Џo�ŎЂɊm�F���A�������邱�Ƃ̊m�F���B
���̎��Ɋ�Â��� |
|
|
�@ |
L��퍐�֘A��Ђ�FDK�Ђ̓����g�����X��JIS�R��C���_�N�^���X280mH |
|
|
�A |
C��IBM�Љt���p�l���̊e�ʂ̎������狁�߂��e�ʂƊ������z�e�ʁA�⏕�e�ʂ̍��v�ł���25pF |
|
|
�B |
R��AMBIT�Ђ���̉ɂ����A�Ɋǂ̃C���s�[�_���X��100K�� |
|
|
�Ƃ��Čv�Z�����Ƃ���A���U���g���͖�60kHz�ƂȂ����i�}�T�|�P�j�B
�����āA���U�̉e���������ɂȂ���g���͋��U���g��60kHz�ɑ��ĒႢ���ɑ���e���͖{���̏ꍇ�A��30kHz������܂ŋy��ł���̂ł���B���̂悤�ɁA���U���ۂ̉e���͈͂Ƃ������̂͋��U���g���𒆐S�Ƃ��Ă��̑O��ɍL���y�ԁB
���������āA�퍐�̎咣�����ɁA�C���o�[�^�̓�����g�������U���g���܂�͋��U�_�œ��삵�Ă��Ȃ����肻��͋��U���Ă���Ƃ͔F�߂Ȃ��Ƃ������̂ł������Ƃ��Ă��A���U���g���ƃC���o�[�^�̓�����g���������ɘ������Ă��Ȃ�����A���U�����Ă��Ȃ��Ƃ������Ƃ͂ł��Ȃ��B |
| �@�Q |
�{���̗͗����P���ʂƌ������̗͗����P���ʂ̈Ⴂ |
|
(1) |
�퍐�͖{�������Z�p�ɂ�����͗����P���ʂɂ��āA�������̗͗����P���ʂƖ{���̗͗����P���ʂ̋�ʂ����Ă���̂��ǂ����s���ȓ_������̂ł���ɂ��ĕ⑫�I�ɏq�ׂ�B |
|
(2) |
�{�������̌��� |
|
|
�g�����X�̏��^���͓�����g�����グ�邱�Ƃɂ������ł��邱�Ƃ͎����̗��ł��邪�A�����ɗ͗��̉��P���ʂ������������g�����X�̏��^���Ɋ�^����B
�����͎����Ȃ��Ƃł��邪�A�͗��̉��P���ʂ�������Δ��M�͌���A����͊����ƃR�A�̗e�ς����炷���Ƃ��Ӗ����A�g�����X�̏��^���ɂȂ�����̂ł���B
�Ƃ��낪�A����炪�������̗͗����P���ʂł���Δ��M�����邱�Ƃ͂Ȃ��A���������ăg�����X�̏��^���ɂ͂Ȃ���Ȃ��B�������̗͗����P���ʂƖ{���̗͗����P���ʂƂ̋�ʂ����邽�߂ɁA�ȉ��ɂ��̌����ɂ��Đ�������B |
|
(3) |
�퍐�͏������ʁi�R�j�X�ł̂Q�P�s�Ȃ����Q�T�s�̒��ŗ͗����P���ʂ͏]���^�̃C���o�[�^�ɂ����݂���Əq�ׂĂ��邪�A����́A��������̗͗����P���ʂ������ė͗����P���ʂ�����̂ł͂Ȃ����Ƃ����A�悭�������Ɋׂ��Ă���\��������̂ŗ\�߉������B |
|
|
�]���^�̃C���o�[�^��H�ɂ����Ă̓g�����X�ꎟ�����猩�����ׂ͈ꎟ�����̎��ȃC���_�N�^���X�����ׂƕ���ɐڑ����ꂽ���̂ƌ��Ȃ���B���Ȃ킿�A�ꎟ�����ɗ����d���͕��ׂ̎��ȃC���_�N�^���X�ɗ����㎥�d���ƕ��ׂɗ�����R�����̓d���Ƃ��������ꂽ�d���ƂȂ�B
�����}�ɂ���Ɛ}�U�|�P�̂悤�ɂȂ�B |
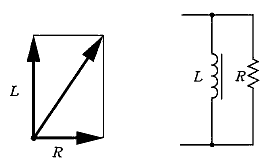
�}6-1 �������̗͗����P���� |
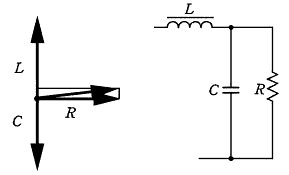
�}6-2 �{���̗͗����P���� |
|
|
|
�d���̃x�N�g�����������Ă��킩��Ƃ���A�㎥�d���ƕ��דd���Ƃ̍����ł͕K�������̗㎥�d��������A����ɂ���ɒ�R���ׂɗ����d���������B
�悭�������̂́A��������ꎟ�����d���ɗ����d���ʑ��́|90�x����0�x�ɋ߂Â��Ă���̂ňꌩ�͗������P����Ă��邩�Ɍ�����B�Ƃ��낪�A����ł͈ꎟ�����ɗ����d���͑����Ȃ邾���ŗ͗��̉��P�ɂ͂Ȃ����Ă�����̂ł͂Ȃ��B
����A�{���̓����Z�p�ɂ�����͗����P�Ƃ͎��̂Ƃ���ł���B�i�}�U�|�Q�j
���ɐڑ����ꂽ�e�ʐ����ɂ��U���������ł�������i�{�����������y0021�z�j�{���ɗ㎥�d���������Ă���B���̌��ʁA�ꎟ�����ɗ����d�������͂قƂ�ǒ�R���דd���݂̂ƂȂ�A�ꎟ�����ɗ����d�������肻�̂��߂ɓ������啝�Ɍ���̂ł���B
C��L�Ƃ̍����d�������S�ɑł������������ꍇ�����U���g���ł���A���g���������قȂ�A�킸���ɑł�������Ȃ��������c���Ă���ꍇ�ł��]���^�ɔ�ׂĂ������I�ȉ��P���ʂ�������̂ł���B |
|
(4) |
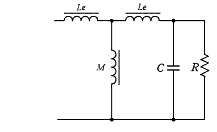
�}6-3 ���ڍׂȃ��f�� |
�g�����X�̗U�������̕������Q�l�܂łɂ��ڍׂɏq�ׂ�ƁA�g�����X�͑��݃C���_�N�^���X���܂O�[�q������H�ɂȂ��Ă���B���̌��ʁA���U���g���ɂ����Ă͑��݃C���_�N�^���X�̕�������������Ď�U�����ɂȂ�B
���̗l�q�̓V�~�����[�V�������ʂɂ��悭����Ă���B |
|
(5) |
���́A�㎥�d����������ʂ������{�������̗͗����P���ʂł��邪�A���̂悤�Ȗ{���̗͗����P���ʂȂ猋�ʂƂ��ăg�����X�̏��^���Ɍ��ʂ�����B |
|
|
�]���̃g�����X�ɂ����Ă͔��M�����炻���Ƃ���A����͈ꎟ�����̊����𑝂₷���A���邢�̓R�A�f�ʐς�傫�����Ĉꎟ�����̎��ȃC���_�N�^���X�𑝂₷���������@���Ȃ��B����͂�������g�����X�̑�^���ɂȂ���B
����A�Y�ƊE�̗v�]�ɂ��g�����X�����^�����Ă����ƁA�ǂ����Ă��R�A�f�ʐς��������Ȃ�ꎟ���������炳�Ȃ���Ȃ�Ȃ��B���̂��Ƃ͈ꎟ�����̎��ȃC���_�N�^���X���������Ȃ�A���̌��ʗ㎥�d���̑����ɂȂ��蓺���������邱�Ƃ��Ӗ�����B
���������āA�]���^�C���o�[�^�̃g�����X�ɂ����Ă̓g�����X�̏��^���ɂ͈��̌��E���������̂ł���B |
|
(6) |
�Ƃ��낪�{�������Z�p�ɂ��Ζ{���I�ȗ͗����P���ʂ�����B |
|
|
���Ȃ킿�A�㎥�d����啝�Ɍ��点��̂ł���B
���̂��߂ɁA�{���̓����Z�p�ɂ����Ă͏]���̂悤�Ɉꎟ�����̃C���_�N�^���X��傫������K�v���Ȃ��Ȃ�A���������āA�ꎟ�����̊��������R�A�f�ʐς��Ƃ��Ɍ��I�ɏ��Ȃ����邱�Ƃ��\�ƂȂ����̂ł���B
�܂��]�k�ł��邪�A�R�A���X�̓g�����X�Ɏg���Ă���R�A�̑̐ςɔ�Ⴗ��B
�{�������Z�p�ɂ��g�����X�̏��^�����\�ɂȂ�ƁA�g�p�����R�A�̐�Ηʂ��啝�Ɍ��邱�ƂɂȂ����̂ŁA���̌��ʕ��Y���Ƃ��ăR�A���X�܂ł����������̂ł���B |
|
(7) |
���������āA�{���̗͗����P���ʂ�����ꂽ����C���o�[�^��H�̃g�����X���������ł����̂ł���A�������̗͗����P���ʂł���Ȃ�g�����X�̏��^���ɂ͂Ȃ���Ȃ��̂ł���B |
|
|
�܂��āA�����P�ɊO���R�A����菜��������g�����X�����^���ł����Ƃ������̂ł��Ȃ��B |
|
(8) |
���̂悤�Ȃ��Ƃ���A�]���^�C���o�[�^��H�ɂ����Ă��͗��̉��P���ʂ�����Ƃ����퍐�̎咣�͏�L�̂悤�Ȍ�������̗͗����P���ʁi�}�U�|�P�j����F���Ă�����̂��A�����͍ŋߏo���]���^��H�̕ό`�ł���R���N�^���U�^�C���o�[�^��H�ɂ����āA���̒��U���g�����C���o�[�^�̓�����g���̂Q�{���O�ł���C���o�[�^��H�̏ꍇ�ŁA���U�ɂ��͗����P���ʁi�}�U�|�Q�j�����������Ă���i�܂�͖{�����N�Q���^����j�悤�ȃC���o�[�^��H�ɂ��ďq�ׂĂ���\���������Ǝv����B |
|
|
������ɂ��Ă��A����炪�{���̗͗����P���ʂȂ̂���������̗͗����P���ʂȂ̂��͏�L�̎��_�ŋ�ʂ��t���ł��낤�B
�{�������Z�p�Ə]���^�Z�p�Ƃ̒��ԂɁA������R�{���U�^�ƌ�����R���N�^���U�^��H�����݂���̂ŎQ�l�܂łɎQ�Ƃ��ꂽ���i�b��T���ؐ}�T�Ȃ����U�j�B�����Ɏg���Ă��钼��R���f���T�͈ꌩ�]���̃o���X�g�R���f���T�Ƌ�ʂ����ɂ����̂Œ��ӂ���K�v�����邪�A����͋��U��H�̈ꕔ���\�����Ă�����̂ł���B |
| �@�R |
�R���f���T�͓d�͂��������̂ł͂Ȃ��B |
|
(1) |
�퍐�͔퍐�������ʁi�R�j�U�ł̂P�W�s�Ȃ����Q�T�s�ɂ����āA�u�e�ʂ����邱�Ƃɂ��]���ȓd�͂�����Ă���v�Əq�ׁA���d�ǎ��ӂɔ�������e�ʂɗ����d�����C���o�[�^��H�̌�����ቺ�����Ă���Ǝ咣���Ă��邪�A���������e�ʂɗ����d���Ƃ������͕̂����̏펯�Ƃ��đ������N�������̂ł͂Ȃ����Ƃ͖����ł���B |
|
|
���������āA���d�ǂ��e�ʂ̌����ƂȂ�t���p�l���ɑg�ݍ��ꍇ�ƁA���d�ǂ��t���p�l��������O���Ċe�ʂ����Ȃ��Ȃ�����ԂƂŔ�r�����ꍇ�ɁA�t���p�l��������O������������d�͂����Ȃ��Ȃ�Ƃ����̂͌��������サ�Ă���킯�ł͂Ȃ��B
���d�ǂ��t���p�l��������O���Ɗe�ʂ��������Ȃ�A���̌��ʃC���o�[�^�̓�����g���������Ȃ�B���̂��߂Ƀg�����X�̂i�h�r�R��C���_�N�^���X�ɂ�郊�A�N�^���X���傫���Ȃ��ĕ��d�ǂɏ\���ȓd�͂������ł��Ȃ��Ȃ邽�߂ɓ��͓d��������̂ł���B |
|
(2) |
�܂��A�C���o�[�^�̓���������啝�ɕω����Ă���̂ł��邩��A�������m���߂邽�߂ɔ퍐�̓C���o�[�^�̓�����g���̏�����Ȃ���Ȃ�Ȃ��B�܂��A���d�ǂ̏���d�͂͒ቺ���Ă���̂őS�����������Ă���̂ł���B |
|
|
���i�ɏq�ׂ�Δ퍐�͑S�����v��p���Ă��ꂼ��̏ꍇ�̑S�����𑪒肵�āA����ƃC���o�[�^�̓��͓d�͂Ƃ��r������Ō������ǂ̂悤�ɕω������̂������Ȃ���ΈӖ����Ȃ��B
�S�����̑���͍���ł���Ύ��P�̍�Ƃ��āA���ꂼ��̏ꍇ�̕��d�ǂɂ�����d���A�d���𑪒肵�A���͓d�͂ɑ���o�͓d�͂̔�Ō����̕ω����c�_����ׂ��ł���B���ʂƂ��Ă�����������ɑ傫�ȕω��͂Ȃ��͂��ł���B
�Ȃ��A���d�ǂ��t���p�l��������O�����ꍇ�ɒ��U���g�����㏸���邱�Ƃ͍b��P�U���ɂ����Ď��؍ς݂ł���B�i�t���p�l���ɑg�ݍ��ꍇ65kHz�A�t���p�l��������O�����ꍇ85kHz�j�B
������ɂ��Ă��A���d�ǂ��t���p�l������O�����ꍇ�ɂ͊e�ʂ̒l���������Ȃ邾���̂��Ƃł���A�퍐���i���e�ʂ𗘗p���Ă��Ȃ����Ƃ̏ؖ��ɂ͂Ȃ�Ȃ��B�ނ���A������g���̕ω��͊e�ʂ𗘗p���Ă��邱�Ƃ̏ؖ��ƂȂ�B |
| �@�S |
�C���_�N�^�͓d�͂��������̂ł͂Ȃ��B |
|
(1) |
�܂��퍐�͔퍐�������ʁi�R�j�P�S�ł̂P�X�s�Ȃ����Q�Q�s�ɂ����āA�u�������ǂ��Ƃ������Ƃ͌����W���i���j�����I�ɂP�ɋ߂����Ƃ��Ӗ�����v�Əq�ׁA�����W�����Ⴂ�g�����X�͌������Ⴂ���̂ƔF�����Ă���悤�ł��邪�A����͂���߂Ċ�b�I�ȊT�O�ɂ����Č��ł���B |
|
|
���ہA�g�����X�ɂ��Ă���قǏڂ����Ȃ��҂͌����W�����Ⴂ�ƕϊ��������Ⴂ�Ɗ��Ⴂ���Ă���ꍇ�����Ȃ��Ȃ����A���̂悤�Ȃ��Ƃ��뜜���Ă��炩���ߌ����͖����Ɂu�����̘R�k��������L�Q�Ȃ��̂ƕ߂炦���{�v����ǎ����^�A�܂�A�d�h���邢�͂d�d�^���̗p����邱�Ƃ����������B�v�Əq�ׂĂ���̂ł���B |
|
(2) |
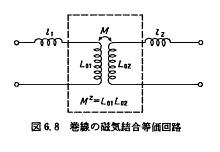
�}7 |
�⑫�܂łɏq�ׂ邪�A�퍐����o��������W���X�O�Ő}6.8�ɂ��������悤�ɁA�R�k�����^�g�����X�Ƃ̓g�����X�̈ꎟ�������A�������ɂ��ꂼ�꒼��ɓ����I�ɃC���_�N�^���}������邾���̘b�ł���B�R�k���������傫���Ƃ́A���̒���ɓ����I�ɑ��݂���C���_�N�^�̒l���傫�����Ƃ��Ӗ�����B |
|
|
�d�C�w��ł͈ꎟ������ѓ��ɓ����I�ɑ��݂��邻�ꂼ��̃C���_�N�^���X���ꎟ���R��C���_�N�^���X�A���R��C���_�N�^���X�ƌĂ�ł���B
����߂Ċ�b�I�Ȃ��Ƃł��邪�A�C���_�N�^�͓d�͂�����Ȃ��̂ł��邩�猋���W�����Ⴍ�Ă��g�����X�̕ϊ��������ቺ������̂ł͂Ȃ��B |
| �@�T |
������g���̖�� |
|
�퍐�͔퍐���i��Lo�i�J���C���_�N�^���X-�퍐�W�L��Ls�j��65kHz�ő��肵�����R�ɂ��āA������C���o�[�^�̓�����g���ł��邩�炾�Ƃ��������Ă��Ȃ����A�����������̎��g���̈�ł͑�����g������kHz�قȂ邾����Lo�̒l���傫���ς��B���̂悤�ɒl���R���R���ς����g���ɂ����đ��肵���l���M�p�ɑ�����̂ł͂Ȃ����Ƃ͖��炩�ł���B
���Ƃ��AJIS C 5321�ɂ͕��z�e�ʂ̉e�����Ȃ����g���ɂ����đ��肹��Ə����Ă���A�퍐�͂i�h�r�̒�߂������������đ��肵�Ă���̂ł���B
���Ȃ݂ɁA�ߔN�̔�����Ă��錴�����i�y�і{�������N�Q���^�킵�����А��i�̃g�����X�̓����ꗗ�\��}�W�Ƃ��Ď����B |
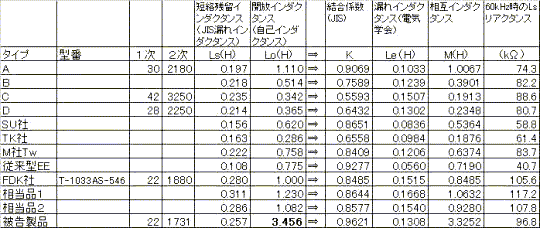
�}�W |
|
|
�퍐�̎咣����A�퍐���i��Lo�i�퍐�W�LLs�j�l���������Б������i�ɔ�ׂēˏo�������l�ł��邱�Ƃ��킩��B����ɂ���Ă��A�퍐�̎���Lo�̐��l�������������Ƃ͖����ł���B |
| �@�U |
�b��P�V���@�ʐ^�U�y�ѐ}�P�O�̃O���t�ɂ��� |
|
�퍐�͍b��P�V���P�P���̎ʐ^�U�y�уO���t�i�}�P�O�j���R�k�����𑪒肵�����̂ł͂Ȃ��A�Əq�ׂ邪�A���̎ʐ^�y�уO���t���R�k�������������̂ł��邱�Ƃ͖����ł���B
���̑���͊ԐړI�ɘR�k�����𑪒肷����̂ł���A���ڂɘR�k�����𑪒肷����̂ł͂Ȃ����A�R�C���Ԃ̓d���̍��͒��ڂɘR�k�����̒l�������Ă���̂ł���i��T�A�Q�́i�T�j�Q�Ɓj�B |
| �@�V |
�o���g�p�X�t�B���^�[�ɂ��� |
|
(1) |
�퍐�͔퍐���i���\������LC��H���o���h�p�X�t�B���^�[���\��������̂ł����āA���U��H���\��������̂ł͂Ȃ��A�Ǝ咣���邪�A���Ƃ��ƃo���h�p�X�t�B���^�[�Ƌ��U��H�Ƃ͂Ƃ��ɔ��ɋߐڂ����Z�p�ł���A����̉�H�ł��邱�Ƃ������̉�H�ł��邱�Ƃ�r�˂�����̂ł͂Ȃ��B |
|
|
�ȒP�Ɍ����Αo���̖ړI���I�[�o�[���b�v���Ă��ăt�B���^�[��H�ł���A���A���̃t�B���^�[��H�͋��U��H�ł��邱�Ƃ̕����ނ����ʓI�ł���B |
|
(2) |
�퍐�����o����MPS�ЋZ�p�����ɂ́AMPS�Ђ�IC���������U�iSPLR�j��H��p����Ɩ�������Ă���킯�ł���A�������������Łu���U�iResonance�j�v�Ƃ����������p�����Ă���ȏ�A�t�B���^�[��H�ł���Ɠ����ɋ��U��H�ł��邱�Ƃ�F�߂Ă���̂ł���B |
|
|
�܂��A�b��P�W����MPS�ЋZ�p�����ɂ����Ă��A�uMP1010�͕��ׂ̋��U���g���ɂ�����������ő���ɂ��v�ƁA������ɋ��U�Z�p��p���邱�Ƃɂ����������P���Ă��邱�Ƃ�PR����Ă���A�퍐���i�Ɏg���Ă���Z�p�����U�Z�p�ł��邱�Ƃ͋^���̗]�n�͂Ȃ��B |
|
(3) |
�Ȃ��A�����͂���ɋ��U���g���ߕӂɂ����鏸�����ʂƃt�B���^�[�����ɂ��ăV�~�����[�V������͂��s�Ȃ��Ă���A���̕��������p����Ƃ��͂����肵�Ă���i�����������ʂS�A�R�T�ł̐}14-7�j�B |
|
|
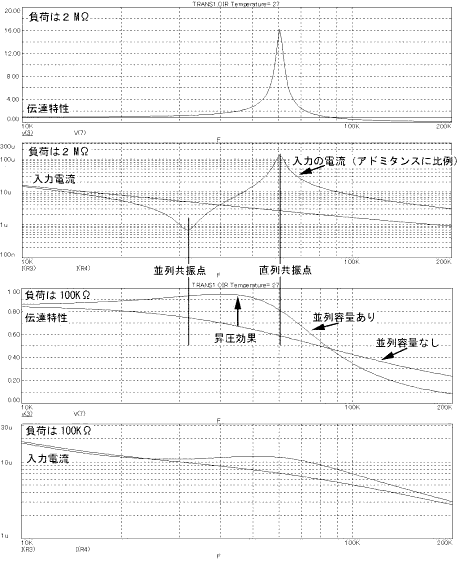
�����������ʂS���}14-7 |
|
|
|
���̃V�~�����[�V�����͒��U���g���t�߂̏������ʂɂ��ĉ�͂��s�Ȃ������̂ł���B
����e�ʂȂ��Ƃ����̂͒��U��H���\�������A���U�ɂ�鏸�����ʂ�S���L���Ȃ��t�B���^�[��H�̏ꍇ�ł���A����e�ʂ���Ƃ͒��U��H�ɂ�鏸�����ʂ�L����t�B���^�[��H�̏ꍇ�ł���B
�����ŏォ��R�Ԗڂ̐}�����Ă��킩��Ƃ���A���U��H���\�����Ă���ꍇ�͋��U��H���\�����Ă��Ȃ��ꍇ�ɔ�ׂĂ��Ȃ�̏������ʂ����邱�Ƃ�������Ă���B
���̂悤�ȃt�B���^�[�����͗�Ƃ��āA�I�[�f�B�I�p�X�s�[�J�[�̃E�[�t�@�i�ቹ�j�ƃX�R�[�J�i�����j�̊ԁA�y�уX�R�[�J�ƃg�D�C�[�^�i�����j�̊Ԃɔ��ɗǂ��g���Ă�����̂ł���A���̂悤�ȃt�B���^�[��H�̂��Ƃ��u���U�ɂ�鏸���ɂ��A�^�[���I�t���������P�����t�B���^�[��H�v�Ƃ����̂ł���B
�ȏ�̂Ƃ���A���U��H�ł��肩�t�B���^�[��H�ł���Ƃ����͎̂��Ɉ�ʓI�Ȃ��Ƃł���A����̉�H�ł��邱�Ƃ������̉�H�ł��邱�Ƃ�r�˂�����̂ł͂Ȃ��B |